Урок 61
Алгоритмически неразрешимые задачи
(§35. Алгоритмически неразрешимые задачи)
Содержание урока
Вычислимые и невычислимые функции
Когда задача алгоритмически неразрешима?
Вычислимые и невычислимые функции
Мы уже говорили, что любой алгоритм задаёт некоторую функцию, которая для каждого входного слова, к которому применим алгоритм, однозначно задаёт результат — выходное слово. Такие функции называются вычислимыми.
Вычислимая функция — это функция, для вычисления которой существует алгоритм.
Любая вычислимая функция может задаваться разными алгоритмами (разными программами для выбранного универсального исполнителя). Например, следующие два нормальных алгорифма Маркова заменяют во входном двоичном слове все буквы «а» на нули и все буквы «б» на единицы:
Любая вычислимая функция может быть вычислена с помощью любого универсального исполнителя: машин Тьюринга и Поста, нормальных алгорифмов Маркова и др.
Рассмотрим, например, такую функцию, определённую для всех натуральных чисел:
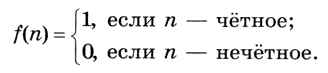
Попробуем составить программу для машины Тьюринга, которая вычисляет эту функцию. Будем считать, что число записано в единичной системе счисления (в виде цепочки единиц 1), и каретка в начальный момент стоит над самой левой единицей. Оказывается, такая программа действительно существует (рис. 5.7).
1 Пустая лента соответствует числу 0.
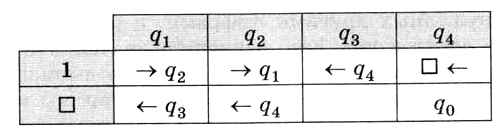
Рис. 5.7
Как принято, в начальный момент машина находится в состоянии q1 Затем она движется вправо вдоль числа, поочередно переходя из состояния q1 (пройдено чётное число единиц) в состояние q2 (пройдено нечётное число единиц) и обратно. Таким образом, если встречен пробел и машина находится в состоянии q2, то число нечётное и нужно просто стереть все единицы (состояние q4). Если машина закончила просмотр в состоянии qv то число чётное; при этом нужно оставить одну единицу (состояние q3) и перейти в состояние q4 (стереть все остальные единицы). Обратите внимание, что ячейка (□, q3) в таблице пустая - это невозможное состояние (покажите это самостоятельно).
Таким образом, рассмотренная функция вычислима, т. е. её можно вычислять с помощью машины Тьюринга, а значит, и с помощью любого универсального исполнителя. Например, нормальный алгорифм Маркова для алфавита А = {1} выглядит так:
В первой подстановке две соседние единицы удаляются (слово-замена здесь пустое, для ясности оно взято в кавычки, которыми можно ограничивать слова в НАМ). Это происходит до тех пор, пока не будут удалены все пары, поскольку эта подстановка стоит первой. Если остаётся одна единица, она удаляется с помощью второй подстановки, и работа программы заканчивается. Если все единицы удалены (число чётное), то с помощью третьей подстановки мы ставим одну единицу и останавливаем автомат.
Существуют и невычислимые функции. Рассмотрим простой пример, предложенный В. А. Успенским в книге «Машина Поста». Известно, что математическая постоянная Пи — иррациональное число, его десятичная запись бесконечна и непериодична. Введем функцию h(n), которая для любого натурального числа n равна 1, если в десятичной записи числа Пи есть n стоящих подряд девяток, окружённых другими цифрами, и равна нулю, если такой цепочки девяток нет. Как вычислить значение этой функции при некотором заданном n? Конечно, можно вычислять друг за другом десятичные знаки числа Пи (такие алгоритмы математикам известны!) и проверять, не нашлась ли в полученной последовательности цифр цепочка из n девяток. С помощью такого «наивного» алгоритма можно найти такие значения n, при которых h(n) = 1: обнаружив требуемую цепочку, алгоритм закончит работу. Например, анализ первых 800 знаков показывает, что h(n) = 1 при n = 0, 1, 2, 6. Но если для какого-то n функция h(n) равна нулю, то «наивный» алгоритм никогда не остановится. Более того, для этой функции вообще не существует алгоритма, который при любом га останавливается и выдает значение h(n) в качестве результата. Поэтому такая функция невычислима.
Следующая страница 
Когда задача алгоритмически неразрешима?
Cкачать материалы урока
