Урок 61
Алгоритмически неразрешимые задачи
(§35. Алгоритмически неразрешимые задачи)

Содержание урока

Вычислимые и невычислимые функции

Когда задача алгоритмически неразрешима?

Вопросы и задания

Задачи

Задачи

1. В качестве доказательства того, что следующая функция вычислима, напишите программу для машины Поста.

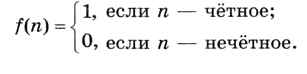
2. Докажите, что следующая функция вычислима:

В качестве доказательства напишите программы для машин Тьюринга и Поста, а также НАМ.

*3. Первой задачей, неразрешимость которой была доказана, была проблема самоприменимости: по заданному тексту программы Р определить, останавливается ли программа Р, если ей на вход подать текст этой же программы. Докажите, что проблема останова сводится к проблеме самоприменимости (именно так и была доказана неразрешимость проблемы останова).

Следующая страница §35. Алгоритмически неразрешимые задачи

Cкачать материалы урока