Урок 63
Доказательство правильности программ
(§37. Доказательство правильности программ)

Содержание урока

Как доказать правильность программы?

Алгоритм Евклида

Инвариант цикла

Спецификация

Вопросы и задания

Задачи

Инвариант цикла

Таким образом, для алгоритма Евклида существует условие НОД(а, b) = НОД(m, n), которое остаётся справедливым на протяжении всего выполнения алгоритма: перед началом цикла, после каждого шага цикла и после окончания работы цикла. Такое условие называется инвариантом цикла (англ. invariant — неизменный).

Инвариант цикла — это соотношение между значениями переменных, которое остаётся справедливым после завершения любого шага цикла.

Выделив в явном виде инвариант каждого цикла, мы избегаем многих возможных ошибок на начальной стадии и делаем первый шаг к доказательству правильности всей программы. Как писал академик Андрей Петрович Ершов, один из первых теоретиков программирования в СССР, «программиста бьют по рукам, если он посмеет написать оператор цикла, не найдя перед этим его инварианта».

Рассмотрим несколько примеров.

Пример 1. Двое играют в следующую игру: перед ними лежат в ряд N + 1 камней, сначала N белых, и в конце цепочки — один чёрный. За один ход каждый может взять от 1 до 3 камней. Проигрывает тот, кто берет чёрный («несчастливый») камень.

Начнём анализ с простейших случаев. Если N — 0, то первый игрок проиграл, он может взять только чёрный камень. Если N = 1, 2, 3, то, наоборот, при правильной игре проигрывает второй игрок, потому что первый может забрать все камни, кроме чёрного. Вариант N = 4 снова приводит к проигрышу первого игрока, потому что забрать все белые камни он не может, а после его хода второй оставит только чёрный камень. Также проигрышными будут позиции при N = 8, 12, 16, ..., т. е. при любых значениях N, которые делятся на 4.

Таким образом, для своего выигрыша игрок должен каждым своим ходом восстанавливать инвариант: число оставшихся белых камней должно быть кратно 4. Если инвариант выполнен в начальной позиции, положение проигрышное и первый игрок может надеяться только на ошибку соперника.

Пример 2. Пусть задан массив А длины n. Найдём инвариант цикла в программе суммирования элементов массива:

Sum:=0

нц для i от 1 до n

Sum:=Sum+A[i]

кц

Здесь на каждом шаге к переменной Sum добавляется элемент массива A[i], так что при любом i после окончания очередного шага цикла в Sum накоплена сумма всех элементов массива с номерами от 1 до i. Это и есть инвариант цикла. Поэтому сразу можно сделать вывод о том, что после завершения цикла в переменной Sum будет записана сумма всех элементов массива.

Аналогично можно показать, что в алгоритме поиска наименьшего значения в массиве:

Min:=А[1]

нц для i от 2 до n

если А[i] < Min то

Min:=A[i]

все

кц

инвариант формулируется так: после выполнения каждого шага цикла в переменной Min записан минимальный из первых i элементов. Отсюда сразу следует, что после завершения цикла (при i = n) в этой переменной будет минимальный из всех элементов.

Пример 3. Для того же массива найдем инвариант цикла в программе сортировки элементов массива методом пузырька:

нц для i от 1 до n-1

нц для j от n-1 до i шаг -1

если A[j] > A[j+l] то

с:= А[j); А(j]:= А[j+1]; A[j + 1]:= с;

все

кц

кц

До начала алгоритма элементы расположены произвольно. На каждом шаге внешнего цикла на свое место «всплывает» один элемент массива. Поэтому инвариант этого цикла можно сформулировать так: «После выполнения i-ro шага цикла первые i элементов массива отсортированы и установлены на свои места».

Теперь построим инвариант внутреннего цикла. В этом цикле очередной «лёгкий» элемент поднимается вверх к началу массива. Перед первым шагом внутреннего цикла элемент, который будет стоять на i-м месте в отсортированном массиве, может находиться в любой ячейке от А[i] до А[n]. После каждого шага его «зона нахождения» сужается на одну позицию, так что инвариант внутреннего цикла можно сформулировать так: «Элемент, который будет стоять на i-м месте в отсортированном массиве, может находиться в любой ячейке от A[i] до А[j]». Очевидно, что когда в конце этого цикла j = i, элемент A[i] встаёт на своё место.

В предыдущих примерах мы определяли инвариант готового цикла. Теперь покажем, как можно строить цикл с помощью заранее выбранного инварианта.

Пример 4. Рассмотрим алгоритм быстрого возведения в степень, основанный на использовании операций возведения в квадрат и умножения. Он использует две очевидные формулы:

(1) a^k = a^k-l • а при нечётной степени k и

(2) а^к = (а²)^k/2 при чётной степени k.

Покажем, как работает алгоритм, на примере возведения числа а в степень 7:

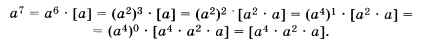
Здесь поочерёдно применяются первая и вторая формулы. Заметим, что на каждом этапе выражение аⁿ можно представить в виде аⁿ = b^к • р, где через р обозначена часть, взятая выше в квадратные скобки. Если нам каким-то образом удастся уменьшить k до нуля, сохранив это равенство, то мы получим аⁿ = р, т. е. задача будет решена, а результат будет находиться в переменной р.

Таким образом, равенство аⁿ = b^к • р можно использовать как инвариант цикла. Для того чтобы обеспечить выполнение этого равенства в начальный момент, можно принять, например, b = а, k = n и р = 1. Далее в цикле применяются формулы (1) и (2) (в зависимости от чётности k на данном шаге). Цикл заканчивается, когда k = 0. В результате получаем следующее решение:

b:=a; k:=n; р:=1

нц пока к <> 0

если mod(k,2)=0 то

к:=div(к,2)

b:=b*b

иначе

к:=к-1

р:=b*р

все

кц

вывод р

Заметим, что инвариант цикла аⁿ = b^к • р выполняется до начала цикла, после каждого шага, а также после завершения цикла. Таким образом, мы написали код программы и одновременно доказали правильность этого блока.

Следующая страница Спецификация

Cкачать материалы урока