Урок 63
Доказательство правильности программ
(§37. Доказательство правильности программ)

Содержание урока

Как доказать правильность программы?

Алгоритм Евклида

Инвариант цикла

Спецификация

Вопросы и задания

Задачи

Спецификация

Для доказательства правильности программы необходимо иметь спецификацию — точное описание того, что должно быть сделано в результате работы программы.

Спецификация — точная и полная формулировка задачи, содержащая информацию, необходимую для построения алгоритма её решения.

На практике спецификации программ обычно формулируют на естественном языке, в котором слова могут иметь несколько разных значений. Для строгого доказательства желательно, чтобы спецификация была задана в формальном виде, с помощью формул или соотношений между величинами.

По предложению английского ученого Ч. Хоара, спецификация записывается в форме {Q}S{R}, где Q — начальное условие, S — программа и R — утверждения, описывающие конечный результат. Запись {Q}S{R} означает следующее: «Если выполнение программы S началось в состоянии, удовлетворяющем Q, то гарантируется, что оно завершится через конечное время в состоянии, удовлетворяющем R».

Корректная программа — это программа, соответствующая спецификации.

Если для исходных данных не удовлетворяется условие Q, программа должна сообщать об этом пользователю и закончить работу. Это говорит о надёжности программы.

Например, для алгоритма Евклида условия Q и R могут выглядеть так:

Q:m ≥ n > 0, R: а = НОД(m,n),

а для программы суммирования элементов массива А[1:n] — так:

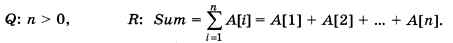
Спецификации могут (и должны) быть составлены не только для программы в целом, но и для её отдельных блоков (процедур, функций, циклов и т. д.). Полезно вносить утверждения Q и R прямо в текст программы. Построенная таким образом аннотированная программа — это ещё один шаг к доказательному программированию.

Ч. Хоар разработал специальный аппарат, позволяющий доказывать правильность программы на основе спецификаций отдельных блоков. Приведём простейшие правила преобразования:

• если {Q}S{P} и Р => R (из истинности Р следует истинность R), то {Q}S{R};
• если {Q}S{P} и R => Q, то {R}S{P};
• если программа S — это последовательное выполнение блоков S₁ и S₂, для которых выполняются спецификации {Q}S₁{P} и {P}S₂{R}, то выполняется спецификация {Q}S{R}.

Доказательство правильности программ используют в двух ситуациях:

• доказывают правильность готовых программ (верификация программ);
• строят программы одновременно с доказательством их правильности (синтез программ).

Как правило, верификация — это очень трудоёмкий и сложный процесс, и оказывается значительно проще использовать доказательства правильности во время разработки программы. При этом программы получаются проще, эффективнее и значительно надёжнее.

Следующая страница Вопросы и задания

Cкачать материалы урока