Уроки 64 - 65
Длинные числа
(§38. Целочисленные алгоритмы)
Содержание урока
Решето Эратосфена
Решето Эратосфена
Во многих задачах все исходные данные и необходимые результаты — целые числа. При этом всегда желательно, чтобы все промежуточные вычисления тоже проводились только с целыми числами. На это есть, по крайней мере, две причины:
• процессор, как правило, выполняет операции с целыми числами значительно быстрее, чем с вещественными;
• целые числа всегда точно представляются в памяти компьютера, и вычисления с ними также выполняются без погрешностей (если, конечно, не происходит переполнение разрядной сетки).
Простые числа широко используются во многих прикладных задачах, например при шифровании с помощью алгоритма RSA (вспомните материал учебника для 10 класса). Основные задачи при работе с простыми числами — это проверка числа на простоту и нахождение всех простых чисел в заданном диапазоне.
Пусть задано некоторое натуральное число N и требуется найти все простые числа в диапазоне от 2 до N. Самое простое (но неэффективное) решение этой задачи состоит в том, что в цикле перебираются все числа от 2 до N, и каждое из них отдельно проверяется на простоту. Например, можно проверить, есть ли у числа k делители в диапазоне от 2 до √k. Если ни одного такого делителя нет, то число k простое.
Описанный метод при больших N работает очень медленно. Греческий математик Эратосфен Киренский (275-194 гг. до н. э.) предложил другой алгоритм, который работает намного быстрее:
1) выписать все числа от 2 до N;
2) начать с k = 2;
3) вычеркнуть все числа, кратные k (2k, 3k, 4k и т. д.);
4) найти следующее невычеркнутое число и присвоить его переменной k;
5) повторять шаги 3 и 4, пока k < N.
Покажем работу алгоритма при N = 16:
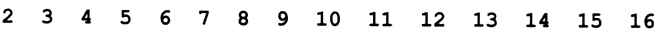
Первое невычеркнутое число — это 2, поэтому вычёркиваем все чётные числа:
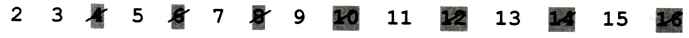
Далее вычёркиваем все числа, кратные 3:
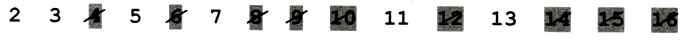
Все числа, кратные 5 и 7, уже вычеркнуты. Таким образом, получены простые числа 2, 3, 5, 7, 11 и 13.
Классический алгоритм можно улучшить, уменьшив количество операций. Заметьте, что при вычёркивании чисел, кратных трём, нам не пришлось вычёркивать число 6, так как оно уже было вычеркнуто. Кроме того, все числа, кратные 5 и 7, к последнему шагу тоже оказались вычеркнуты.
Предположим, что мы хотим вычеркнуть все числа, кратные некоторому k, например k = 5. При этом числа 2k, 3k и 4k уже были вычеркнуты на предыдущих шагах, поэтому нужно начать не с 2k, а с k2. Тогда получается, что при k2 > N вычёркивать уже будет нечего, что мы и увидели в примере. Поэтому можно использовать улучшенный алгоритм:
1) выписать все числа от 2 до N;
2) начать с k = 2;
3) вычеркнуть все числа, кратные k, начиная с k2;
4) найти следующее невычеркнутое число и присвоить его переменной k;
5) повторять шаги 3 и 4, пока k2 ≤ N.
Чтобы составить программу, нужно определить, что значит «выписать все числа» и «вычеркнуть число». Один из возможных вариантов хранения данных — массив логических величин с индексами от 2 до N. Как и в учебнике 10 класса, слева будем писать программу на школьном алгоритмическом языке, а справа — на языке Паскаль.
Объявление переменных в программе будет выглядеть так (для N = 100):

Если число i не вычеркнуто, будем хранить в элементе массива A[i] истинное значение, если вычеркнуто — ложное. В самом начале нужно заполнить массив истинными значениями:
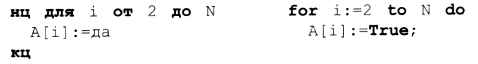
В основном цикле выполняется описанный выше алгоритм:
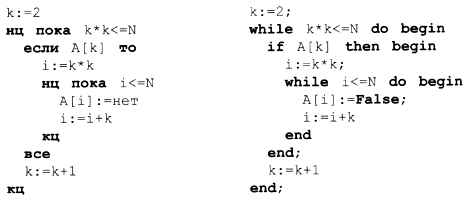
Обратите внимание, что для того, чтобы вообще не применять вещественную арифметику, мы заменили условие k ≤ √N на равносильное условие k2 ≤ N, в котором используются только целые числа.
После завершения этого цикла невычеркнутыми остались только простые числа, для них соответствующие элементы массива содержат истинные значения. Эти числа нужно вывести на экран:
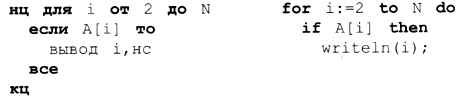
Следующая страница  «Длинные» числа
«Длинные» числа

