Уроки 64 - 65
Длинные числа
(§38. Целочисленные алгоритмы)
Содержание урока
«Длинные» числа. Задача
«Длинные» числа. Задача
Задача. Вычислить точно значение факториала 100! = 1 • 2 • 3 • ... • 99 • 100 и вывести его на экран в десятичной системе счисления (это число состоит более чем из сотни цифр и явно не помещается в одну переменную).
Для хранения «длинного» числа будем использовать целочисленный массив А. Определим необходимую длину массива. Заметим, что
1 • 2 • 3 • ... • 99 • 100 < 100100.
Число 100100 содержит 201 цифру, поэтому число 100! содержит не более 200 цифр. Если в каждом элементе массива записано 6 цифр, для хранения всего числа требуется не более 34 элементов:
Чтобы найти 100!, нужно сначала присвоить «длинному» числу значение 1, а затем последовательно умножать его на все числа от 2 до 100. Запишем эту идею на псевдокоде, обозначив через [А] «длинное» число, находящееся в массиве А:
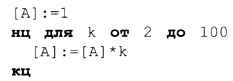
Записать в «длинное» число единицу — значит присвоить элементу А[0] значение 1, а в остальные переменные записать нули:
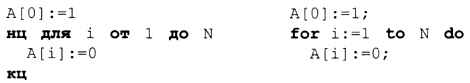
Таким образом, остаётся научиться умножать «длинное» число на «короткое» (k ≤ 100). «Короткими» обычно называют числа, которые помещаются в переменную одного из стандартных типов данных.
Попробуем сначала выполнить такое умножение на примере. Предположим, что в каждом элементе массива хранятся 6 цифр «длинного» числа, т. е. используется система счисления с основанием d = 1 000 000. Тогда число [А]=12345678901734567 хранится в трёх элементах:
Пусть k = 3. Начинаем умножать с младшего разряда: 734567 • 3 = 2203701. В нулевом разряде могут находиться только 6 цифр, значит, старшая двойка перейдёт в перенос в следующий разряд. В программе для выделения переноса r можно использовать целочисленное деление на основание системы счисления d. Остаток от деления — это то, что остаётся в текущем разряде. Поэтому получаем:
Для следующего разряда будет всё то же самое, только в первой операции к произведению нужно добавить перенос из предыдущего разряда, который был записан в переменную r. Приняв в самом начале r = 0, запишем умножение «длинного» числа на «короткое» в виде цикла по всем элементам массива, от А[0] до A[W]:
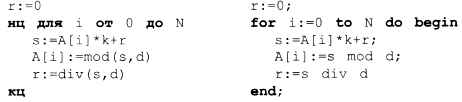
В свою очередь, эти действия нужно выполнить в другом (внешнем) цикле для всех k от 2 до 100:
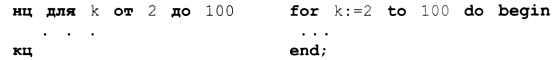
После этого в массиве А будет находиться искомое значение 100!, остаётся вывести его на экран. Нужно учесть, что в каждой ячейке хранятся 6 цифр, поэтому в массиве
хранится значение 1000002000003, а не 123. Кроме того, старшие нулевые разряды выводить на экран не надо. Поэтому при выводе требуется:
1) найти первый (старший) ненулевой разряд числа;
2) вывести это значение без лидирующих нулей;
3) вывести все следующие разряды, добавляя лидирующие нули до 6 цифр.
Поскольку мы знаем, что число не равно нулю, старший ненулевой разряд можно найти в таком цикле 1:
1 Подумайте, что изменится, если выводимое число может быть нулевым.
Старший разряд выводим обычным образом (без лидирующих нулей):
вывод А[i] write(A[i]);
Для остальных разрядов будем использовать специальную процедуру Write6:
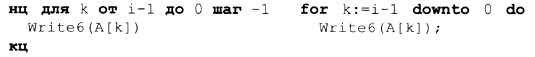
Эта процедура последовательно выводит цифры десятичного числа, начиная с сотен тысяч и кончая единицами:
Для того чтобы разобраться, как она работает, выполните «ручную прокрутку» при различных значениях х (например, возьмите х = 1, х = 123 и х = 123456).
Следующая страница 
Вопросы и задания
Cкачать материалы урока
