Урок 8
Использование графов
(§7. Системный подход в моделировании)

Содержание урока

Введение

Табличные модели

Диаграммы

Диаграммы. Задачи 1 и 2

Иерархические модели

Сетевые модели

Игровые стратегии

Вопросы и задания

Задачи с 1 по 8

Задачи с 9 по 16

Игровые стратегии

Как вы уже знаете из § 6, игровые модели — это модели, которые описывают соперничество двух (или более) сторон, каждая из которых стремится к выигрышу, т. е. преследует свою цель. Часто цели участников противоречивы — выигрыш одного означает проигрыш других.

Построением и изучением игровых моделей занимается теория игр — раздел прикладной математики. Задача состоит в том, чтобы найти стратегию (алгоритм игры), который позволит тому или другому участнику получить наибольший выигрыш (или, по крайней мере, наименьший проигрыш) в предположении, что соперники играют безошибочно.

Во многих простых играх, в которых игроки ходят по очереди, есть не так много вариантов развития событий, и их можно рассмотреть полностью, однозначно определив, кто выиграет в заданной начальной ситуации, если оба соперника не будут ошибаться.

Все позиции (игровые ситуации) делятся на выигрышные и проигрышные. Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если сам не сделает ошибку. При этом говорят, что у него есть выигрышная стратегия — алгоритм выбора очередного хода, позволяющий ему выиграть.

Если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник. В этом случае говорят, что у него нет выигрышной стратегии. Таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника.

Выигрышные и проигрышные позиции можно охарактеризовать так:

• позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная;
• позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.

Для примера рассмотрим игру с камнями, в которой участвуют два игрока. Вначале перед игроками лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу один камень (ход «+1») или увеличить количество камней в куче в два раза (ход «*2»). Например, имея кучу из 5 камней, за один ход можно получить кучу из 6 или 10 камней. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 14 камней или больше.

Рассмотрим возможный результат игры при разном начальном количестве S камней в куче. Очевидно, что при S < 6 первый игрок (т. е. игрок, делающий первый ход) выигрывает сразу, удвоив число камней в куче. Начнём заполнять таблицу, в которой для каждого значения S будем указывать, выигрышная это позиция или проигрышная, и через сколько ходов завершается игра:

Здесь «В₁» обозначает выигрыш за один ход.

При S = 6 у первого игрока есть два хода: ход «+1» даёт кучу из 7 камней, а ход «*2» — кучу из 12 камней. Выиграть за один ход он не может, оба возможных хода ведут в выигрышные (для второго!) позиции, поэтому первый игрок проиграет, если второй не ошибётся. Позицию S = 6 отметим в таблице как «х₁» (проигрыш за 1 ход):

Вспомним, что задача игрока — перевести игру в проигрышную для соперника позицию. Если S = 5 или S = 3, первый игрок может получить (ходом «+1» или «*2» соответственно) кучу из 6 камней, т. е. создать проигрышную позицию. Этого достаточно для выигрыша, но выиграть можно только за 2 хода:

Рассуждая аналогично, выясняем, что позиция S = 4 — проигрышная, так как возможные ходы ведут в выигрышные позиции (соперник выиграет за 1 или за 2 хода). При S = 2 первый игрок может своим ходом «*2» перевести игру в проигрышную позицию (S — 4), поэтому он выиграет. А при S = 1 он проиграет, потому что может своим ходом получить только кучу из 2 камней:

Полученная таблица показывает результат игры первого игрока в том случае, если второй не будет ошибаться. Если игра начинается в проигрышной позиции, первый игрок проиграет, а если в выигрышной — его стратегия состоит в том, чтобы на каждом шаге своим ходом создавать проигрышную позицию для соперника.

Для полного исследования всех вариантов игры можно построить дерево, содержащее все возможные ходы. Предположим, что сначала в куче 4 камня (эта позиция будет корнем дерева). Тогда в результате первого хода может получиться куча из 5 или 8 камней:

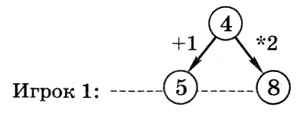
Следующий уровень дерева показывает все возможные позиции после ответного хода второго игрока:

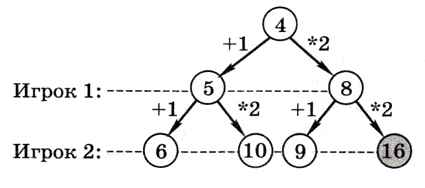
Мы видим, что второй игрок может выиграть своим первым ходом (получив 16 камней), если первый построит кучу из 8 камней. В остальных случаях игра продолжается, и дерево можно строить дальше по тому же принципу.

Как мы уже показали ранее с помощью таблицы, при S = 4 выигрывает второй игрок. Чтобы доказать это с помощью дерева, не нужно строить полное дерево игры. Достаточно рассмотреть все возможные ходы соперника и для каждого из них найти один (!) выигрышный ход второго игрока. Вариант с выигрышем в один ход мы уже разобрали, теперь посмотрим, что произойдёт, если первый игрок получит кучу из камней.

Как следует из построенной выше таблицы, для кучи из 5 камней выигрышный ход второго игрока — «+1», он переводит игру в проигрышную позицию. При любом ответе первого игрока второй выигрывает своим вторым ходом «*2»:

Таким образом, мы доказали, что при S = 4 у второго игрока есть стратегия, позволяющая ему гарантированно выиграть, по крайней мере, за 2 хода.

Следующая страница Вопросы и задания

Cкачать материалы урока