Урок 8
Использование графов
(§7. Системный подход в моделировании)
Содержание урока
Задачи с 9 по 16
Задачи с 9 по 16
9. Путешественник прибыл в посёлок Моховое в полночь по местному времени и увидел следующее расписание автобусов.
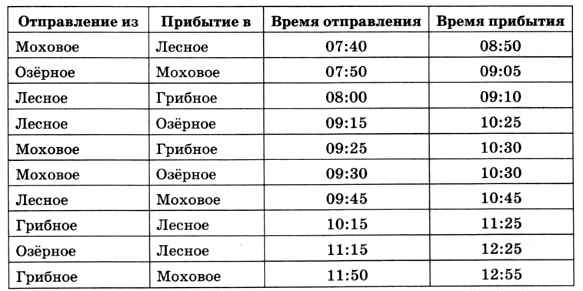
Определите самое раннее время, когда он может попасть в посёлок Лесное, и как ему нужно ехать.
10. На диаграмме показано, сколько ноутбуков, МРЗ-плейеров и телевизоров продала некоторая фирма в первые три месяца года (I квартал).
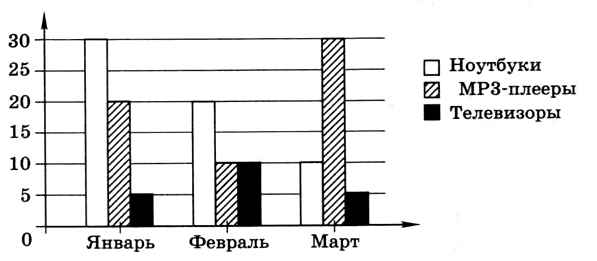
Какая из следующих диаграмм правильно отражает соотношение общего количества проданных товаров разных видов за весь I квартал?

11. В соревнованиях участвовали спортсмены из Москвы, Санкт- Петербурга и Мурманска, каждый из них имеет III, II или I разряд. На диаграмме 1) показано количество спортсменов, имеющих разные разряды, а на диаграмме 2) — соотношение спортсменов из разных городов.

Какие из этих утверждений следуют из анализа диаграмм:
а) все спортсмены, имеющие П разряд, могут быть москвичами;
б) все спортсмены из Мурманска могут иметь II разряд;
в) все спортсмены из Санкт-Петербурга могут иметь I разряд;
г) все спортсмены III разряда могут быть из Москвы?
12. В салоне продаются автомашины «Лада», «УАЗ» и «Ока» трёх цветов: красного, синего и зелёного. На диаграмме 1) показано количество машин разного цвета, а на диаграмме 2) — количество машин разных марок.
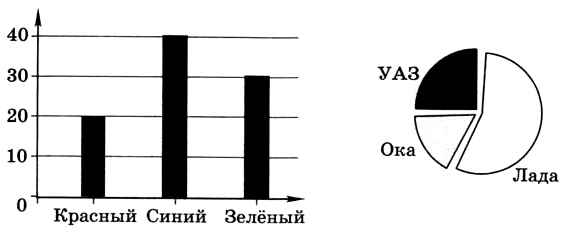
Какие из этих утверждений следуют из анализа диаграмм:
а) все автомобили «УАЗ» — зелёные;
б) среди автомобилей «Ока» нет красных;
в) все автомобили «Ока» — синие;
г) среди автомобилей «Лада» есть синие?
13. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 2 камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 25 камней или больше. Для каждого значения S (1 ≤ S ≤ 24) определите, кто выиграет и за сколько ходов. Для S = 7 постройте дерево игры, показывающее стратегию выигрывающего игрока.
14. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 1 камень или увеличить количество камней в куче в три раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 55 камней или больше. Для каждого значения S (1 ≤ S ≤ 54) определите, кто выиграет и за сколько ходов. Для S = 16 постройте дерево игры, показывающее стратегию выигрывающего игрока.
15. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу два камня, добавить в кучу три камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 30 камней или больше. Для каждого значения S (1 ≤ S ≤ 29) определите, кто выиграет и за сколько ходов. Для S = 9 постройте дерево игры, показывающее стратегию выигрывающего игрока.
16. Игра Баше. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может взять из кучи 1, 2 или 3 камня. Выигрывает тот, кто возьмет последний камень. Для каждого значения S (1 ≤ S ≤ 15) определите, кто выиграет и за сколько ходов. Для S = 12 постройте дерево игры, показывающее стратегию выигрывающего игрока.
Следующая страница  §7. Системный подход в моделировании
§7. Системный подход в моделировании

