Уроки 15 - 18
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)
Содержание урока
Модель неограниченного роста
Модель неограниченного роста
Многие идеи в области моделирования были предложены биологами. Достаточно вспомнить, что родоначальником общей теории систем (системного подхода) был биолог Людвиг фон Берталанфи. В этом параграфе мы познакомимся с моделями некоторых биологических систем.
Одна из задач, которые решают биологи, — изучение изменения численности животных в некоторой области. Обычно их пересчитывают раз в год, поэтому модель изменения численности получается дискретной — с её помощью можно определить численность с интервалом 1 год.
Обозначим через N0 начальную численность, а через Ni — численность в i-й год с момента начала наблюдений. Количество родившихся и умерших животных пропорционально численности, поэтому годовой прирост равен kp • Ni - kc • Ni, где kp и kc — коэффициенты рождаемости и смертности. Тогда количество животных в (i + 1)-й год может быть вычислено через их количество Ni в предыдущему году:
Ni+1 = Ni + kp • Ni - kc • Ni = (1+ K) • Ni,
где К = kp - kc — коэффициент прироста. Это и есть математическая модель развития популяции («населения») животных. Коэффициенты kp и kc (так же как и другие коэффициенты в рассматриваемых далее моделях) обычно определяются экспериментально.
При К = 0 (рождаемость равна смертности) количество животных не меняется, при К < 0 (kp < kc) животные вымирают, а при К > 0 (kp > kc) их число бесконечно увеличивается (рис. 2.14).
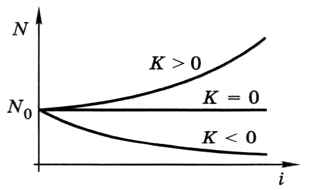
Рис. 2.14
Поэтому эту модель называют моделью неограниченного роста.
Английский учёный и экономист Томас Мальтус использовал её для описания роста населения Земли, поэтому эту модель иногда называют моделью Мальтуса.
Недостаток этой модели в том, что она не учитывает ограниченность ресурсов (например, пищи), влияние других видов и изменяющихся природных условий, из-за которых изменяются коэффициенты рождаемости и смертности. Поэтому модель Мальтуса адекватна только при небольших интервалах наблюдения.
Следующая страница  Модель ограниченного роста
Модель ограниченного роста

