Уроки 15 - 18
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)

Содержание урока

Модель неограниченного роста

Модель ограниченного роста

Взаимодействие видов

Обратная связь. Саморегуляция

Вопросы и задания

Задачи

Модель ограниченного роста

Бельгийский математик Пьер Ферхюльст предложил ввести максимальную численность популяции L и построить модель так, чтобы численность животных не превышала этой величины. Как только численность приближается к L, коэффициент прироста уменьшается и рост замедляется. Модель Ферхюльста основана на той же самой формуле, что и модель Мальтуса:

N_i+1 = (1 + K_L) • N_i,

но теперь коэффициент прироста K_L зависит от численности N_i:

K_L = K • (L - N_i / L),

где К — начальный коэффициент (при нулевой численности). Видно, что при увеличении N_i коэффициент K_L уменьшается и при N_i = L становится равен нулю.

Нередко человек искусственно разводит животных, например, в рыбоводческих хозяйствах или на зверофермах. В этом случае ежегодно часть животных (обозначим её R) отлавливается, а оставшиеся размножаются и поддерживают популяцию. Для того чтобы определить допустимый отлов, при котором популяция сохраняется (не вымирает), используют модель с отловом:

N_i+1 = (1 + K_L) • N_i, K_L = K • (L - N_i / L).

На рисунке 2.15 показаны графики изменения численности популяции для разных моделей при N₀ = 100, К = 0,5, L = 1000 и R = 40. Видно, что в самом начале модели ограниченного и неограниченного роста дают близкие результаты, т. е. модель неограниченного роста адекватна.

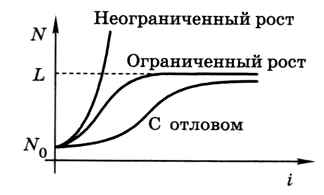
Рис. 2.15

Согласно модели ограниченного роста, со временем численность популяции приближается к L, а при отлове устанавливается численность немного меньше L. Вы можете рассчитать это значение самостоятельно, приняв, что в состоянии равновесия N_i+1 = N_i.

Следующая страница Взаимодействие видов

Cкачать материалы урока