Урок 7
§5. Основные сведения об алгоритмах

5.1. Свойства алгоритма.

Значение слова «алгоритм» очень похоже по значению на слова «рецепт», «метод», «способ». Но, в отличие от рецепта или способа, любой алгоритм обязательно обладает следующими свойствами.

1. Дискретность. Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно действие, можно приступать к выполнению следующего. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.

2. Детерминированность. Каждая команда алгоритма определяет однозначное действие исполнителя и недвусмысленно указывает, какая команда должна выполняться следующей. Если алгоритм многократно применяется к одному и тому же набору входных данных, то каждый раз получаются одинаковые промежуточные и выходной результаты.

3. Понятность. Алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неоднозначно, т. е. запись алгоритма должна быть настолько чёткой и полной, чтобы у исполнителя не возникло потребности в принятии каких-либо самостоятельных решений. Стоит помнить, что алгоритм всегда рассчитан на выполнение «неразмышляющим» исполнителем.

4. Результативность. Под этим свойством понимается содержательная определённость результата каждого шага и алгоритма в целом. При точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет. Свойство результативности содержит в себе свойство конечности — завершение работы алгоритма за конечное число шагов.

5. Массовость. Алгоритм пригоден для решения любой задачи из некоторого класса задач, т. е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма.

Докажите, что рассмотренный в примере 2 метод Эратосфена является алгоритмом.

Не любой расписанный по шагам способ решения задачи является алгоритмом. Убедимся в этом на примере.

Пример 3. Опишем метод построения перпендикуляра к прямой MN, проходящего через заданную точку А этой прямой, с помощью линейки и циркуля (рис. 2.2):

1) отложить в обе стороны от точки А на прямой MN циркулем отрезки равной длины с концами В и С;
2) увеличить раствор циркуля до радиуса, в полтора-два раза больше длины отрезков АВ и АС;
3) провести указанным раствором циркуля дуги окружностей с центрами в точках В и С так, чтобы они охватили точку А и образовали две точки пересечения друг с другом (В и Е);
4) взять линейку, приложить её к точкам В и В и соединить их отрезком; при правильном построении отрезок пройдёт через точку А и будет являться перпендикуляром к прямой MN.

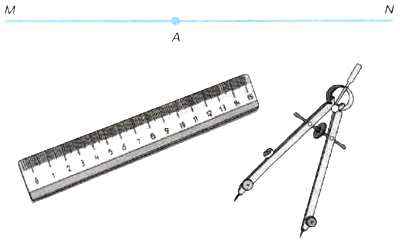
Рис. 2.2. Построение перпендикуляра к прямой

Почему этот способ построения перпендикуляра к прямой не является алгоритмом? Какое свойство алгоритмов здесь нарушено?

Есть задачи, которые человек успешно решает, но при этом не может представить процесс их решения в виде последовательности шагов.

Например, если перед человеком положить фотографии собак и кошек и попросить определить, на каких фотографиях изображены собаки, а на каких кошки, то человек практически мгновенно и безошибочно решит эту задачу. Написать же формальный алгоритм решения этой и подобных ей задач пока что не удалось, хотя определённые успехи в этой области, называемой теорией распознавания образа, уже достигнуты.

В супермаркетах вы видите системы распознавания штрих-кодов, используете системы оптического распознавания символов, знаете о распознавании автомобильных номеров, слышали о распознавании изображений лиц, речи и т. д.

Технические системы распознавания образов находят сегодня широкое применение в самых разных областях — от военного дела и систем безопасности до оцифровки аналоговых сигналов. Их разработка базируется на теории распознавания образов — разделе информатики и смежных дисциплин, развивающем основы и методы классификации и идентификации предметов, явлений, процессов, сигналов, ситуаций и тому подобных объектов, характеризующихся конечным набором некоторых свойств и признаков.

С учётом рассмотренных свойств алгоритма можно дать более формальное определение этого понятия, которое также не является строгим, т. к. в нём всё ещё используются не определяемые точно термины.

Алгоритм — это конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и обладает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.

Математики достаточно долго пользовались интуитивным (нестрогим) понятием алгоритма, записывая алгоритмы примерно так, как в примере 3. Ими были сформулированы многие успешно применяемые на практике алгоритмы решения таких задач, как выполнение арифметических действий «столбиком», нахождение корней квадратных и кубических уравнений, решение систем линейных уравнений и др. Постепенно математики подходили к постановке и решению всё более сложных задач, требовавших построения формального определения алгоритма.

Попытки разработать формальное определение алгоритма привели в 20-30-х годах XX века к возникновению теории алгоритмов — науки, изучающей общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. Вместе с математической логикой теория алгоритмов образует теоретическую основу вычислительных наук.

Математики (А. Тьюринг, Э. Пост, А. Н. Колмогоров, А. А. Марков и др.) предложили несколько подходов к формальному определению алгоритма: нормальный алгоритм Маркова, машина Тьюринга, машина Поста и т. д. Дальнейшее показало, что все эти определения эквивалентны. На основании этих определений учёные пришли к выводу о существовании алгоритмически неразрешимых задач — задач, для которых невозможно построить процедуру решения.

Cкачать материалы урока