Урок 7
§5. Основные сведения об алгоритмах

5.2. Способы записи алгоритма

Из курса информатики основной школы вам известны разные способы записи одного и того же алгоритма:

• словесная запись алгоритма на естественном языке;
• запись алгоритма псевдокодом — частично формализованным естественным языком с элементами языка программирования и общепринятыми математическими обозначениями;
• запись алгоритма в виде блок-схемы — подробного графического представления логической структуры программы или алгоритма с помощью стандартных блоков (условных символов), соединённых линиями;
• запись алгоритма на языке программирования и т. д.

Выбор способа записи алгоритма зависит от ряда причин. Небольшой алгоритм можно записать и в словесной форме. Если для вас наиболее важна наглядность, то разумно использовать блок-схему. Алгоритм же, готовый к реализации, должен быть записан на языке, понятном исполнителю.

Правила выполнения блок-схем, внешний вид графических блоков и их назначение определяются стандартом ГОСТ 19.701-90 (ИСО 5807-85) «Схемы алгоритмов, программ, данных и систем. Обозначения условные и правила выполнения».

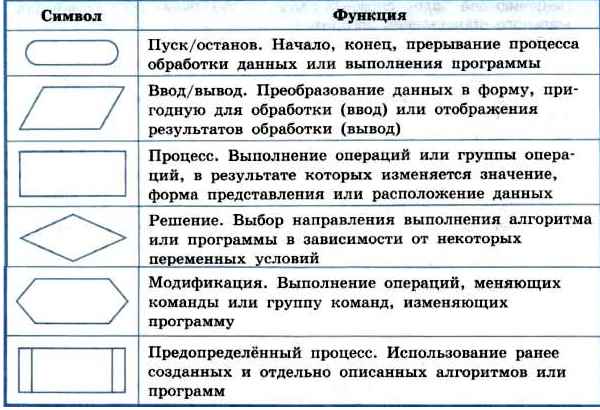
Напомним основные условные графические обозначения (символы), которые мы будем использовать в дальнейшем (табл. 2.1).

Таблица 2.1

Основные символы блок-схем и отображаемые ими функции

Пример 4. Вспомним детскую игру «Угадай-ка». Первый игрок задумывает целое число и сообщает второму игроку, из какого оно диапазона. Второй игрок должен как можно быстрее угадать загаданное число. Второй игрок может называть числа, а первый должен говорить, меньше или больше названное число задуманного. Игра заканчивается, если названо число, равное задуманному.

Пусть задумано число X ∈ [А, В]. Представим в виде блок-схемы алгоритм решения этой задачи — известный вам метод половинного деления (рис. 2.3).

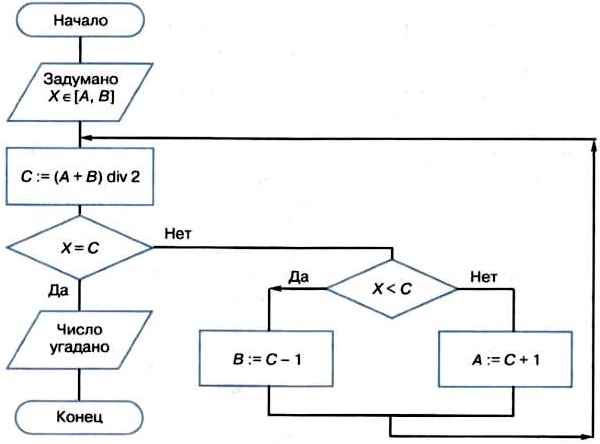
Рис. 2.3. Метод половинного деления

Подсчитайте, какое наибольшее число шагов может понадобиться для угадывания по этому алгоритму числа X ∈ [0, 100].

Cкачать материалы урока