Урок 9
§7(1, 2). Запись алгоритмов на языке программирования Паскаль

7.2. Некоторые сведения о языке программирования Pascal (продолжение)

Пример 1. В начале этой главы мы обсуждали алгоритмы нахождения простых чисел. Напишем программу, проверяющую, является ли заданное натуральное число п простым.

Самый простой путь решения этой задачи — проверить, имеет ли данное число n (n >= 2) делители в интервале [2; n - 1].

Если делители есть, число n — составное, если — нет, то — простое.

В программе будем использовать логическую переменную flag:

• если flag = true, то n — простое число;
• если flag = false, то n — составное число (если у числа n есть делители, то «флаг выключаем» с помощью оператора присваивания flag := false).

В этой программе мы проверяли, нет ли у числа n делителей из интервала [2; n - 1]. Но если п = а • Ь, то меньшее из чисел а, b не больше 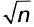(в противном случае оба числа были бы больше 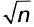, а следовательно, их произведение было бы больше n). Кроме того, из делимости числа n на а автоматически следует, что n делится и на n/а.

Усовершенствуйте приведённую выше программу с учётом этих соображений.

Проверку, является ли заданное натуральное число n >= 2 простым, мы осуществили методом перебора всех возможных его делителей. Метод перебора используется для решения достаточно широкого круга задач.

Пример 2. Применим метод перебора для поиска наибольшего общего делителя (НОД) двух натуральных чисел а и b.

Начнём перебор с d — наименьшего из чисел а и Ь. Это первый, очевидный кандидат на роль их наибольшего общего делителя. И далее, пока не найдём d, на которое оба числа делятся нацело, будем уменьшать его на единицу. Как только такое деление произойдёт, останавливаем уменьшение d. Полученное значение d и будет наибольшим общим делителем чисел а и Ь.

Cкачать материалы урока