Уроки 31 - 34
§1.10. Графы и их исследование с использованием языков объектно-ориентированного программирования Visual Basic и Turbo Delphi

Содержание урока

1.10.1. Введение в теорию графов

Основные понятия теории графов

Маршрут графа

Ориентированные графы

Взвешенные графы

Описание графа с помощью матрицы смежности

Подграфы и деревья

Преобразование графа в основное связное дерево минимального веса

Контрольные вопросы

1.10.2. Изучение графов на языке Visual Basic

1.10.3. Изучение графов на языке Turbo Delphi

1.10.1. Введение в теорию графов

Основные понятия теории графов

При проектировании компьютерных сетей, телефонных линий, трубопроводов и строительстве дорог необходимо минимизировать затраты на прокладку коммуникаций. Прежде всего, целесообразно выбрать минимальный по длине маршрут прокладки коммуникаций.

Например, необходимо соединить телефонным или компьютерным кабелем шесть зданий, расстояния между которыми различны (рис. 1.57). Возникает задача определения маршрута прокладки кабеля минимальной длины, но при этом подходящего к каждому зданию. Для решения таких задач часто используют теорию графов.

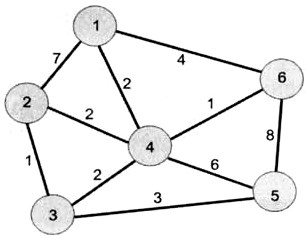
Рис. 1.57. Задача прокладки коммуникаций

Основные понятия теории графов. Граф G задается с помощью пары множеств G = (V,R), где V — множество (совокупность) вершин, R — множество ребер, соединяющих пары вершин. Множество ребер может быть пустым, если ни одна из вершин не соединена с другими вершинами.

Обычно граф представляют с помощью схемы, на которой некоторые вершины соединены линиями (ребрами) (рис. 1.58).

Вершинами могут служить объекты любой природы будь то населенные пункты, компьютеры сети, элементы блок-схем алгоритмов и т. д. Под ребрами могут подразумеваться дороги между двумя соседними городами, стороны геометрических фигур, линии связи между компьютерами.

Любую систему улиц в городе можно представить в вид» графа. Здесь вершины — это перекрестки.

Вершины называются смежными, если их соединяет ребро. Например, на рис. 1.58 смежные вершины V₁ и V₂, так как их соединяет ребро R₁₂.

Множества V и R являются конечными — мы можем перечислить все вершины и ребра графа. Количество вершин и количество ребер графа определяют мощности множеств V и R. Так, количество вершин графа G равно 5, а количество ребер равно 8.

Ребро и любая из его двух вершин называются инцидентными. Под степенью вершины подразумевается количество инцидентных ей ребер. Так, степень вершины V₁ равна 3, а степень вершины V₅ равна 4.

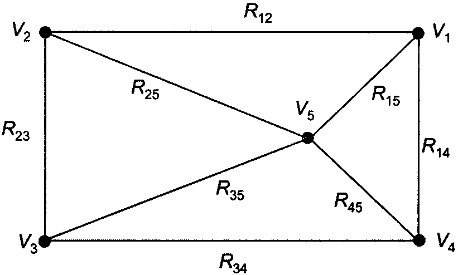
Рис. 1.58. Граф G в форме схемы

Следующая страница Маршрут графа

Cкачать материалы урока