Уроки 31 - 34
§1.10. Графы и их исследование с использованием языков объектно-ориентированного программирования Visual Basic и Turbo Delphi
Содержание урока
1.10.1. Введение в теорию графов
Основные понятия теории графов
Описание графа с помощью матрицы смежности
Преобразование графа в основное связное дерево минимального веса
1.10.2. Изучение графов на языке Visual Basic
1.10.3. Изучение графов на языке Turbo Delphi
1.10.1. Введение в теорию графов
Преобразование графа в остовное связное дерево минимального веса
Пусть G = (V, R) — связный взвешенный неориентированный граф, где V — множество вершин, a R — множество ребер (см. рис. 1.58). Ребра графа не ориентированы, т. е. ребра Rnk и Rkn считаются одним и тем же ребром, поэтому в матрице смежности не учитываются дублирующие друг друга ребра. В результате граф G можно представить с помощью матрицы смежности, содержащей значения весов десяти ребер (на рис. 1.61 выделены жирным шрифтом).
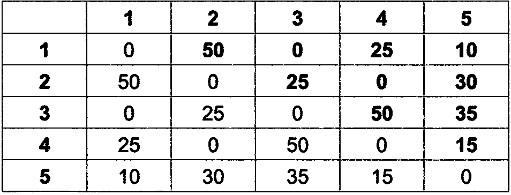
Рис.1.61. Матрица смежности связного взвешенного неориентированного графа G
Введем понятие цикломатического числа ϒ, показывающего, сколько ребер графа нужно удалить, чтобы в нем не осталось ни одного цикла. Цикломатическое число ϒ равно увеличенной на единицу разности между количеством ребер и количеством вершин графа:
ϒ = m - n + 1,
где m — количество ребер, n — количество вершин.
Например, для графа, изображенного на рис. 1.58, цикломатическое число равно:
ϒ = m - n + 1 = 8 - 5 + 1 = 4.
Это значит, что для получения остовного связного дерева в графе G необходимо убрать четыре ребра, и тогда в нем не останется ни одного цикла.
Для каждого графа обычно существует несколько остовных связных деревьев, которые обладают различными весами. На рис. 1.60, в представлено остовное связное дерево графа G, вес которого равен 135, а на рис. 1.62 представлены три остовных связных дерева графа G, веса которых равны 130, 100, 135.

Рис. 1.62. Остовные связные деревья графа G
Для построения остовного связного дерева минимального веса используется алгоритм Крускала.
1. Первоначально из графа удаляются все ребра, получается остовной подграф, где все вершины изолированы. Каждая вершина такого графа помещается в одноэлементное подмножество.
2. Ребра сортируются по возрастанию весов.
3. Ребра последовательно, по возрастанию их весов, включаются в основное дерево. Существуют четыре случая:
а) обе вершины включаемого ребра принадлежат одноэлементным подмножествам, тогда они объединяются в новое, связное подмножество;
б) одна из вершин принадлежит связному подмножеству, а другая нет, тогда включаем вторую в подмножество, которому принадлежит первая;
в) обе вершины принадлежат разным связным подмножествам, тогда объединяем подмножества;
г) обе вершины принадлежат одному связному подмножеству, тогда исключаем данное ребро.
4. Алгоритм заканчивает работу, когда все вершины будут объединены в одно множество, при этом оставшиеся ребра не включаются в остовное дерево.
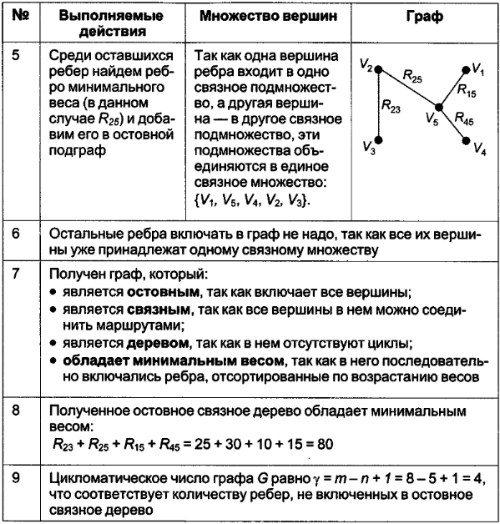
Рассмотрим реализацию этого алгоритма на примере построения остовного дерева минимального веса для графа G.

Следующая страница  Контрольные вопросы
Контрольные вопросы

