Уроки 31 - 34
§1.10. Графы и их исследование с использованием языков объектно-ориентированного программирования Visual Basic и Turbo Delphi
Содержание урока
1.10.1. Введение в теорию графов
1.10.2. Изучение графов на языке Visual Basic
1.10.3. Изучение графов на языке Turbo Delphi
Проект «Построение остовного связного дерева графа» на языке Turbo Delphi
Событийная процедура вывода в графическое поле вершин графа
Событийная процедура вывода элементов матрицы смежности взвешенного ориентированного графа
Событийная процедура вывода элементов матрицы смежности взвешенного неориентированного графа
Событийная процедура построения остовного связаного дерева минимального веса
1.10.3. Изучение графов на языке Turbo Delphi
Событийная процедура построения остовного связаного дерева минимального веса
Событийная процедура построения остовного связного дерева минимального веса. В этой процедуре пользователь строит остовное связное дерево минимального веса. Ребро минимального веса выбирается с использованием матрицы смежности неориентированного графа. Ввод номеров вершин ребра минимального веса осуществляется с помощью функции ввода данных InputBox(). Включение или невключение выбранного ребра в остовное дерево производится на основании пункта 3 алгоритма Крускала, который реализуется с использованием функции вывода сообщений MessageDlg () и оператора условного перехода в сокращенной форме.
В результате остовное связное дерево минимального веса будет нарисовано в графическом поле, веса ребер будут выведены в таблицу, а суммарный вес ребер — на надпись.
10. Щелкнуть по кнопке Button4 и в заготовку событийной процедуры ввести программный код:
procedure TForm1.Button4Click(Sender: TObject);
begin
//Ввод номера первой вершины и ее рисование
//в графическом поле
strN:=InputBox('Выбор ребра минимального веса', 'Введите номер первой вершины:',' ');
Image2.Canvas.Pen.Width:=3;
Image2.Canvas.Ellipse(X[StrToInt(strN)],
Y[StrToInt(strN)],X[StrToInt(strN)]+ 4,
Y[StrToInt(strN)]+4);
Image2.Canvas.TextOut(X[StrToInt(strN)]+5,
Y[StrToInt(strN)],strN);
//Ввод номера второй вершины и ее рисование
//в графическом поле
strK:=InputBox(’Выбор ребра минимального веса',’Введите номер второй вершины:',’’);
Image2.Canvas.Pen.Width:=3;
Image2.Canvas.Ellipse(X[StrToInt(strK)],
Y[StrToInt(strK)],X[StrToInt(strK)]+4,
Y [StrToInt(strK)]+4);
Image2.Canvas.TextOut(X[StrToInt(strK)]+5,
Y [StrToInt(strK)],StrK);
//Реализация пункта 3 алгоритма Крускала
A:=MessageDlg(’Ребро с вершинами ’ + StrN +
’ и ’ + StrK + ’ включить в состав
остовного дерева, если выполняется хотя бы одно из условий: (Обе вершины не входят
в остовное дерево) или (Одна из вершин не входит в остовное дерево) или (Вершины
входят в различные подмножества остовного дерева).’, MtConfirmation,[mbYes,mbNo], 0);
If A=mrYes
Then
begin
Image2.Canvas.Pen.Width:=1;
Image2.Canvas.MoveTo(X[StrToInt(strN)],
Y[StrToInt(strN)]);
Image2.Canvas.LineTo(X[StrToInt(strK)],
Y[StrToInt(StrK)]);
R1[StrToInt(strN),StrToInt(strK)]:=
Round(Sqrt(Sqr(X[StrToInt(strN)]-X[StrToInt(strK)])+
Sqr(Y[StrToInt(strN)]-Y [StrToInt(strK)])));
StringGrid3.Cells[StrToInt(strN), StrToInt(strK)]:=
IntToStr(R1[StrToInt(strN),
StrToInt(strK)]);
S:=R1[StrToInt(strN, StrToInt(strK))]+S;
Label1.Caption:=IntToStr(S);
end;
end;
На основе анализа матрицы смежности неориентированного графа выберем ребро минимального веса.
11. Осуществить щелчок по кнопке Остовное связное дерево.
В появившемся диалоговом окне Выбор ребра минимального веса ввести номер первой точки и щелкнуть по кнопке ОK (рис. 1.75).
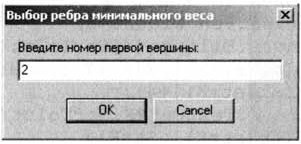
Рис. 1.75. Ввод первой вершины графа
12. В появившемся диалоговом окне Выбор ребра минимального веса ввести номер второй точки и щелкнуть по кнопке ОK (рис. 1.76).
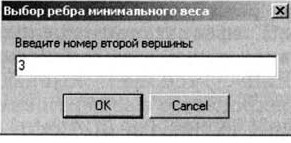
Рис. 1.76. Ввод второй вершины графа
На основе анализа остовного связного дерева в графическом поле выполним пункт 3 алгоритма Крускала и решим вопрос о включении или невключении выбранного ребра в остовное дерево.
13. В появившемся диалоговом окне Confirm подтвердить или опровергнуть истинность условий щелчком по кнопке Yes или по кнопке No (рис. 1.77).
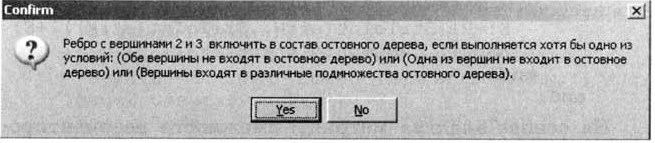
Рис. 1.77. Включение ребра в состав остовного дерева
14. Выполнять пункты 11-13 до тех пор, пока остовное связное дерево с минимальным весом не будет построено, т. е. пока все вершины не войдут в связное множество.
В результате (рис. 1.78):
• в графическом поле будет построено остовное связное дерево;
• в соответствующие ячейки таблицы будут выведены веса ребер остовного дерева;
• на надпись будет выведена сумма весов ребер остовного связного дерева минимального веса.
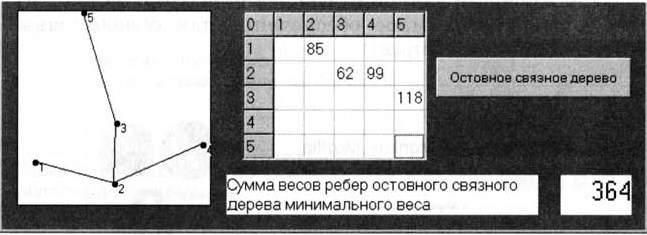
Рис. 1.78. Остовное дерево минимального веса
Следующая страница  Контрольные вопросы
Контрольные вопросы

