В алгоритмическом языке есть функция выделения целой части числа: int(x). Нужно иметь в виду, что функция trunc в Паскале отбрасывает дробную часть, а функция int в алгоритмическом языке находит целую часть по правилам математики — как наибольшее целое число, не превосходящее данное. Поэтому для отрицательных чисел они дают разные результаты:

вывод int (-1.5) | = -2 write(trunc(-1.5)); { = -1 }

Функция frac(x) в языке Паскаль выделяет дробную часть вещественного числа х.

Как можно выделить дробную часть положительного вещественного числа в алгоритмическом языке?

Что будет выведено на экран в результате работы следующей программы?

Чтобы извлечь квадратный корень из числа, т. е. найти такое число, квадрат которого равен заданному, применяют функцию sqrt. Вот так можно найти квадратный корень из числа 5:

вывод sqrt(5):0:3 | = 2.236 write(sqrt(5):0:3); { = 2.236}

Операции div и mod к вещественным числам неприменимы.

Напишите программу, которая вычисляет квадратный корень введённого числа. Вычислите с её помощью квадратные корни из чисел 221841; 32005,21 и 15239,9025.

Вычисления с вещественными числами могут давать неточные результаты. Вспомните, что число 1/3 не может быть точно записано в десятичной системе — его дробная часть содержит бесконечное число цифр. В компьютерах происходит то же самое: на каждое число выделяется конечное число разрядов, поэтому большинство вещественных чисел хранится в памяти компьютера неточно. Следовательно, вычисления тоже будут неточными.

Вычислите сумму 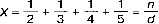в виде простои дроби.

Проверьте, что выведет эта программа (вместо многоточий добавьте полученные значения n и d):

Сделайте выводы.

Следующая страница Случайные и псевдослучайные числа

Cкачать материалы урока

Уроки 26 - 29§18. Линейные программы

Содержание урока

Операции с вещественными числами

Уроки 26 - 29
§18. Линейные программы