Урок 15
§10. Другие логические операции

Содержание урока

Импликация

Эквиваленция

Исключающее ИЛИ

Шифрование

Выводы

Вопросы и задания

Практическая работа № 8 «Шифрование»

Импликация

• импликация
• исключающее ИЛИ
• эквиваленция

Мы изучили две логические операции с двумя переменными — Ии ИЛИ. Существуют ли другие? И сколько их?

В таблице истинности любой логической операции с двумя переменными всего четыре строки, и эти таблицы отличаются только четырьмя значениями функции в последнем столбце. Поэтому можно придумать всего 16 = 2⁴ различных логических операций с двумя переменными.

На уроках математики вы доказывали теоремы, в которых встречались выражения «если ..., то...», «тогда и только тогда, когда...». Эти связки тоже обозначают логические операции, с которыми мы сейчас и познакомимся.

Слово «импликация» означает «следование» — из одного утверждения следует другое. Если истинно первое, то истинно и второе. Например, возьмём высказывание

X = Если идёт дождь, то Лена раскрывает зонтик.

Если ввести обозначения для простых высказываний:

А = Идёт дождь,

В = Лена раскрывает зонтик, то можно записать высказывание X в символьном виде:

X = А → В.

Стрелка вправо обозначает логическую операцию «импликация».

Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «импликация». Что оно означает?

Теперь давайте разберёмся, когда такое высказывание будет истинно, а когда — ложно. Если дождь идёт (А = 1) и Лена раскрывает зонтик (В = 1), то импликация, очевидно, истинна. Если же при дожде Лена зонтик не раскрыла, импликация ложна (из А не следует B!).

А если дождя нет (А = 0)? Тогда о состоянии зонтика Лены мы ничего сказать не можем, потому что он может быть как закрыт, так и открыт. И в обоих случаях импликация будет истинна, потому что не исключено, что из А следует В (возможно, что, когда пойдёт дождь, Лена откроет зонтик). Говорят, что "из истины следует истина, а из лжи — что угодно"

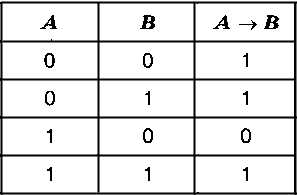
Рис. 2.13

Таблица истинности операции импликация показана на рис. 2.13. Как видим, эта функция равна нулю только при одном значении исходных данных: 1 → 0 = 0, во всех остальных случаях она равна 1.

Обычно, говоря «если..., то...», мы имеем в виду причинно-следственную связь, когда одно вызывает другое. Например, «Если светит солнце, то лужи высыхают» (именно потому, что светит солнце!). Импликация не говорит о причине и следствии, а показывает возможность такой связи. Например, может быть истинной импликация «если сегодня вторник, то Эльбрус покрыт снегом».

Импликация часто используется при решении логических задач. Например, формулировку вида «если А, то В» можно записать как А → В = 1.

Постройте таблицу истинности логической функции В → А ¹⁾. Сравните её с таблицей истинности функции А → B. Выполняется ли для импликации переместительный закон (если поменять местами А и B, то результат не изменяется)?

¹⁾ В этой и следующих трёх задачах сохраняйте порядок столбцов в таблице истинности: в первом столбце записывайте значение А, во втором — значение B.

Постройте таблицу истинности логической функции А + B. Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы сейчас доказали?

Постройте таблицу истинности логической функции B → А. Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы сейчас доказали?

Постройте таблицу истинности логической функции (А → В) и (В → А). Как бы вы назвали эту функцию?

Следующая страница Эквиваленция

Cкачать материалы урока