Уроки 16 - 18
§11. Логические выражения

Содержание урока

Формализация

Таблицы истинности

Составление условий

Логические схемы

Выводы

Вопросы и задания

Таблицы истинности

Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения

X = А и не В или не А и B,

которое можно также записать в виде

X = А • B + А • В.

Сколько строк в таблице истинности выражения с двумя переменными?

Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).

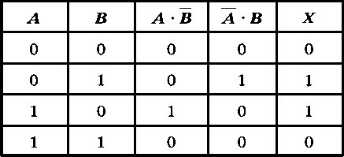
Рис. 2.18

Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.

Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.

Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.

Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.

Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?

Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.

Сколько строк в таблице истинности выражения с тремя переменными?

Постройте таблицу истинности логического выражения

Х = А • В + А • С + В • С.

Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).

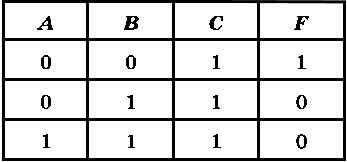
Рис. 2.19

Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?

Всего в таблице истинности функции от трёх переменных 2³ = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.

Сколько различных значений можно закодировать с помощью 5 бит?

Как вы нашли это значение?

Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:

а) А + В + C;

б) A • С + В;

в) А + B • С;

г) А • В • C;

д) A • B + C.

Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.

Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.

Проверьте самостоятельно, подходят ли остальные варианты.

Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:

а) А + B + C;

б) A • С • В;

в) А • B • C;

г) A + В + С;

д) A + B + C.

Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).

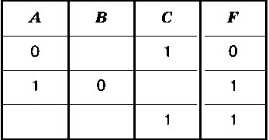
Рис. 2.20

Выясним, какие из следующих функций могут соответствовать этой таблице:

а) A + В + C;

б) A • С • В;

в) А + B + C;

г) А • B • С;

д) А + В + C.

Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:

а) 1 + В + 0;

в) 0 + B + 0;

д) 0 + В + 0.

Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.

Кратко решение можно записать так:

1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;

2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;

3) этим условиям удовлетворяют функции в) и д).

Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).

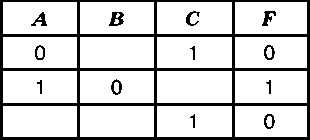
Рис. 2.21

Выясните, какие из следующих функций могут соответствовать этой таблице:

а) А • B + C;

б) A • С • В;

в) А + B + C;

г) А • B • С;

д) А + B + C.

Следующая страница Составление условий

Cкачать материалы урока