Урок 19
§12. Множества и логика

Содержание урока

Множества

Диаграммы Эйлера-Венна

Количество элементов во множестве

Сложные запросы в поисковых системах

Выводы

Вопросы и задания

Диаграммы Эйлера-Венна

Множества удобно изображать графически, в виде диаграмм. Их называют диаграммами Эйлера—Венна в честь авторов этой идеи — математика Леонарда Эйлера и логика Джона Венна. На такой диаграмме каждому множеству соответствует какая-то область (круг, прямоугольник и др.) — рис. 2.34. Все элементы внутри этой области принадлежат множеству, все элементы вне области — не принадлежат.

Рис. 2.34

Вы уже знаете, что множество можно задать условием (логическим выражением), которое выполняется для всех элементов множества и не выполняется для всех элементов, не входящих в него. Дальше для сокращения записи мы будем вместо слов «множество, для которого выполняется условие А» писать просто «множество А». Тогда множество «НЕ А» на диаграмме — это все точки за границами круга (рис. 2.35).

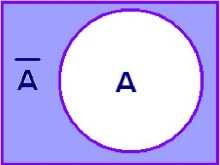
Рис. 2.35

Такое множество называется дополнением множества А до универсального множества U, включающего все элементы некоторого класса. Например, если мы рассматриваем только целые числа и А — это множество чётных целых чисел, то А — множество нечётных целых чисел.

Можно считать, что дополнение А — это «разность» между универсальным множеством U и множеством А, т. е. все элементы из U, которые не входят в А.

Для каждого из следующих множеств выберите универсальное множество и запишите дополнение А:

а) А = {1, 3, 5, 7, 9};
б) А = {а, е, ё, и, о, у, ы, э, ю, я};
в) А = {17, 34, 51, 68, 85};
г) А = {00, 10};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С};
е) А = отрезок [0; 1].

На диаграмме можно изображать несколько множеств, каждому из них соответствует своя область (круг). Круги на диаграмме могут пересекаться. Элементы, расположенные в общей части кругов А и В, — это пересечение множеств А и В. Для этих элементов выполняется как условие А, так и условие В, т. е. выполняется условие А и В (А • В) — рис. 2.36.

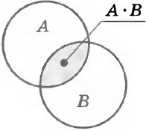
Рис. 2.36

Если круги не пересекаются (множества не содержат общих элементов), их пересечение — это пустое множество ∅.

Для пары множеств определите пересечение А • В:

а) А = {1, 3, 5, 7, 9}, В = {1, 5, 6, 9, 12};
б) А = {а, б, в, г, д, е, ё, ж}, В = {а, е, ё, и, о, у, ы, э, ю, я};
в) А = {17, 34, 51, 68, 85}, В = {17, 34, 51, 68, 85};
г) А = {00, 10}, В = {01, 11};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С}, В = {А, В, С, D, Е, F, G, Н};
е) А = [5; 15], В = [10; 20];
ж) А = [5; 15], В = [0; 20];
з) А = [5; 15], В = [10; 12];
и) А = [5; 15], В = [20; 30].

Элементы, входящие хотя бы в одно из множеств: в А или в В, образуют новое множество, которое называется объединением множеств А и В. Для всех элементов этого множества выполняется условие А или В (А + В) — рис. 2.37.

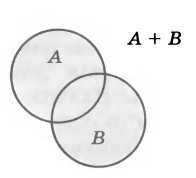
Рис. 2.37

Для пары множеств определите объединение А + В:

а) А = {1, 3, 5, 7, 9}, В = {1, 5, 6, 9, 12};
б) А = {а, б, в, г, д, е, ё, ж }, В = {а, е, ё, и, о, у, ы, э, ю, я};
в) А = {17, 34, 51, 68, 85}, В = {17, 34, 51, 68, 85};
г) А = {00, 10}, В = {01, 11};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С}, В = {А, В, С, D, Е, F, G, И};
е) А = [5; 15], В = [10; 20];
ж) А = [5; 15], В = [0; 20];
з) А = [5; 15], В = [10; 12];
и) А = [5; 15], В = [20; 30].

Подобные диаграммы можно нарисовать для любого логического выражения, ведь каждое из них определяет некоторое множество. Например, возьмём выражение А + В. Оно равно 0 только при А = 1 и В = 0, поэтому на диаграмме незакрашенной останется только область, которая входит в круг А и не входит в круг В (рис. 2.38).

Рис. 2.38

В тетради постройте диаграммы для логических выражений:

а) А + B;
б) А • B + А • В;
в) А • B + А • B.

Диаграмма для трёх переменных содержит три круга, каждый из которых (в общем случае) пересекается с двумя другими (рис. 2.39).

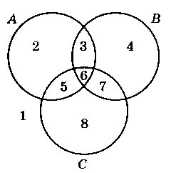
Рис. 2.39

Для удобства на рис. 2.39 области пронумерованы. Запишем, для примера, логическое выражение для области 3. Эта область находится внутри кругов А и B (следовательно, выражения А и B истинны), но вне круга С, поэтому выражение С ложно. Получается условие А и B и (не С), или, в других обозначениях, А • B • C.

Запишите в тетради логические выражения для остальных областей на рис. 2.39.

Для того чтобы найти выражение для объединения двух или нескольких областей, надо сложить (используя логическое сложение — операцию ИЛИ) выражения для всех составляющих. Например, выражение для объединения областей 3 и 4 на рис. 2.39 имеет вид:

3 + 4:А • В • C + А • В • C.

Вместе с тем точки в этих областях отличаются от других тем, что они входят в область Б и не входят в область С. Поэтому справедлива более простая формула:

3 + 4: B • C.

Это означает, что логические выражения в некоторых случаях можно упростить.

Следующая страница Количество элементов во множестве

Cкачать материалы урока