Уроки 32 - 41
Оператор ветвления. Логические операции на Паскале
(§ 12. Алгоритмы с ветвящейся структурой. § 13. Программирование ветвлений на Паскале. § 14. Программирование диалога с компьютером)
Разработка программы на языке Паскаль с использованием оператора ветвления и логических операций
Содержание урока
Уроки 32 - 33. Алгоритмы с ветвящейся структурой
Уроки 32 - 33. Сложные ветвящиеся алгоритмы
Уроки 32 - 33. Вопросы и задания
Уроки 32 - 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 1 - 6)
Уроки 32 - 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 7 - 12)
Уроки 32 - 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 13 - 19)
Уроки 34 - 35. Программирование ветвлений на Паскале
Уроки 36 - 37. Программирование диалога с компьютером
Уроки 32 - 33
Сложные ветвящиеся алгоритмы
Получим алгоритм решения еще одной задачи: найти наибольшее значение среди трех величин: А, В, С.
Естественно, возникает следующая идея этого алгоритма: сначала нужно найти большее из значений А и B и присвоить его какой-то дополнительной переменной, например D; затем найти большее среди D и С. Это значение можно присвоить той же переменной D.
Решение задачи сводится к двукратному применению уже знакомого алгоритма нахождения большего из двух значений. Блок-схема алгоритма — на рис. 2.5.
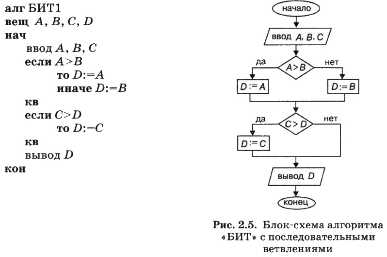
Нетрудно догадаться, что «БИТ» обозначает «Большее из трех». В структуре этого алгоритма содержатся два последовательных ветвления: первое — полное, второе — неполное.
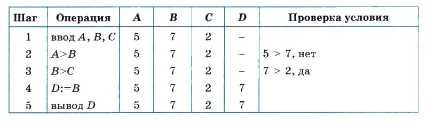
Эту же задачу можно решить с помощью алгоритма, имеющего структуру вложенных ветвлений. Его блок-схема приведена в следующем параграфе на рис. 2.6. А вот как выглядят описание этого алгоритма на АЯ и трассировочная таблица при А = 5, B = 7, С = 2.
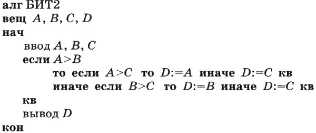
Коротко о главном
В команде ветвления в качестве условия может использоваться отношение неравенства между величинами.
Числовые величины, которые могут принимать целые и дробные значения, имеют вещественный тип.
Для решения одной и той же задачи можно построить несколько вариантов алгоритмов.
Несколько ветвлений в одном алгоритме могут быть последовательными и вложенными.
Вопросы и задания
1. Какую структуру имеет алгоритм нахождения большего из двух значений?
2. Почему отношение неравенства можно назвать логическим выражением?
3. В каком случае для числовой переменной следует указывать целый тип, в каком — вещественный?
4. Составьте алгоритм (в виде блок-схемы и на АЯ) нахождения меньшего из двух значений.
5. Составьте алгоритм нахождения наименьшего из трех значений.
6. Для вывода на экран произвольной символьной строки нужно в команде вывода записать эту строку в кавычках. Например, по команде
вывод "ОТВЕТ"
на экран выведется слово ОТВЕТ.
Определите, какая задача решается по следующему алгоритму.

7. Составьте алгоритм, по которому на компьютере будет происходить следующее: в переменную S вводится возраст Саши, в переменную М вводится возраст Маши. В качестве результата на экран выводится фраза «Саша старше Маши» или «Маша старше Саши» (предполагаем, что кто-нибудь из них обязательно старше).
8. Решите предыдущую задачу, учитывая возможность одинакового возраста Саши и Маши. В таком случае может быть получен ответ: «Саша и Маша — ровесники».
9. Составьте алгоритм упорядочения значений трех переменных по возрастанию, т. е. при любых исходных значениях А, B, С отсортируйте их так, чтобы стало: А ≤ В ≤ С. Проверьте алгоритм трассировкой при разных вариантах значений исходных данных.


