Урок 111
Точность вычислений
§69. Точность вычислений
Содержание урока
Погрешности измерений
Погрешности измерений
«Недостатки математического образования с наибольшей отчётливостью проявляются в чрезмерной точности численных расчётов», — писал выдающийся немецкий математик первой половины XIX века Карл Фридрих Гаусс.
Все практические расчёты выполняются неточно, с некоторой погрешностью (ошибкой, отклонением от истинного значения). В первую очередь это связано с тем, что неточно известны исходные данные, которые получаются в результате измерений.
Окружающие нас предметы имеют различные числовые характеристики (длину, массу, объём и др.), которые часто приходится измерять для решения практических задач. Для измерений используются приборы, каждый из которых имеет определённую точность. Это значит, что с помощью данного прибора невозможно зафиксировать изменение величины, меньшее, чем цена деления шкалы этого прибора. Поэтому измеренное значение величины всегда отличается от точного (истинного), разность между ними называют погрешностью измерения.
Пусть нужно найти толщину дна кружки, используя только линейку с ценой деления 1 мм. Линейкой можно измерить высоту кружки снаружи и глубину внутри (рис. 9.1). При этом точность измерений будет не выше чем 1 мм (0,1 см). Например, если измеренная высота кружки оказалась примерно 8,2 см, на самом деле она может быть от 8,1 до 8,3 см. Если измеренная глубина равна 7,8 см, фактическая может быть от 7,7 до 7,9 см.
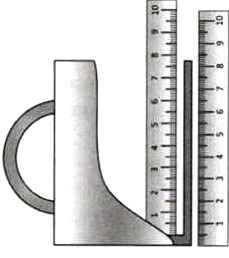
Рис. 9.1
Используя данные измерений, можно найти толщину дна как разность
8,2 - 7,8 = 0,4 см.
Это не означает, что толщина дна действительно такая. Действительно, с учётом ошибок измерений она может быть равна как 8,1 - 7,9 = 0,2 см, так и 8,3 - 7,7 = 0,6 см. Таким образом, реальная толщина может быть от 0,2 до 0,6 см (разница в 3 раза!), и в полученном ответе (0,4 см) нет ни одной верной значащей цифры! Обычно в этом случае пишут ответ в виде 0,4 ± 0,2 см.
В приведённом примере погрешность 0,2 см — это так называемая абсолютная погрешность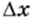 
. Для оценки качества измерений чаще используют относительную погрешность, которая вычисляется как отношение абсолютной погрешности Дх к истинному значению величины х*:
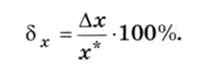
Поскольку истинное значение, как правило, неизвестно, его обычно заменяют на полученный результат изменений. В данном случае относительную погрешность можно оценить как
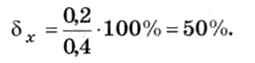
Это очень большое значение, которое говорит о низкой точности измерений.
Следующая страница 
Погрешности вычислений
Cкачать материалы урока
