Урок 111
Точность вычислений
§69. Точность вычислений
Содержание урока
Погрешности вычислений
Погрешности вычислений
Пусть нужно вычислить площадь сечения цилиндра, диаметр которого D — 1,2 см известен с точностью 0,1 см. По известной формуле площади круга получаем (например, на калькуляторе):
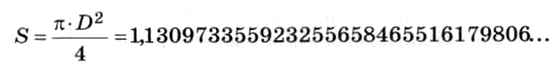
Рис. 9.2
Значит ли это, что мы нашли площадь с такой точностью? Конечно, нет. Вспомним, что диаметр был измерен с точностью 0,1 см, т. е. он мог быть в самом деле равен как 1,1 см, так и 1,3 см. В этих «крайних» случаях получаем площадь
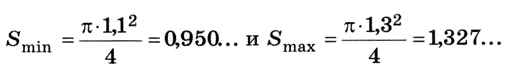
Таким образом, следует записать ответ в виде S ≈ 1,1 ± 0,2 см2.
Относительную погрешность результата можно оценить как
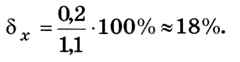
Заметим, что мы не учитывали погрешность, связанную с неточностью задания иррационального числа π.
Все практические расчёты выполняются неточно. Погрешность результата вычислений определяется в первую очередь погрешностью исходных данных.
Теперь вернёмся к расчётам с помощью компьютера. Как вы знаете из главы 4, данные записываются в память в двоичном коде ограниченной длины, при этом практически все вещественные числа хранятся неточно. При выполнении вычислений погрешности накапливаются, поэтому при сложных расчётах может получиться неверный ответ. Например, с точки зрения точности очень плохо, если ответ — это небольшое (по модулю) число, которое вычисляется как разность двух неточных больших чисел (вспомните пример с кружкой!).
Погрешность резко возрастает при делении на неточное малое по модулю число. Предположим, что нужно вычислить значение
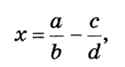
причём а, b, с и d — вещественные числа, которые получены в результате вычислений с погрешностью 0,001: a = 1000 ± 0,001; b = 0,002 ± 0,001; с = 1000 ± 0,001; d = 0,003 ± 0,001.
Легко проверить, что вычисленное значение х может находиться в интервале от -166 667 до 750 001, т. е. относительная погрешность превышает 300%! Такой метод расчётов вычислительно неустойчив: малые погрешности в исходных данных могут привести к огромным погрешностям в решении.
Подводя итог, можно выделить несколько источников погрешностей при компьютерных вычислениях:
• неточность исходных данных;
• неточность записи вещественных чисел в двоичном коде конечной длины;
• погрешности приближённого вычисления некоторых стандартных функций (например, sin(x) или cos(x));
• накопление погрешностей при арифметических действиях с неточными данными;
• собственная погрешность используемого метода (для приближённых методов, рассматриваемых в следующем параграфе).
Проблемы, возникающие при вычислениях с конечной точностью, изучает вычислительная математика, задача которой — разработать вычислительно устойчивые методы решения задач, при которых небольшие погрешности исходных данных мало влияют на результат. Иногда этого удаётся добиться простым изменением порядка действий или преобразованием формул.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
