Уроки 115 - 116
Дискретизация. Вычисление длины кривой и площадей фигур
§71. Дискретизация
Содержание урока
Вычисление длины кривой
Вычисление длины кривой
Определим длину траектории L, по которой летит шарик, брошенный под углом к горизонту (см. задачу в § 70). Это не так просто, потому что траектория — кривая линия.
Постараемся как-то свести задачу к более простой, которую мы умеем решать. Если бы линия состояла из отдельных отрезков, её длину можно было бы точно вычислить с помощью теоремы Пифагора. Например, длина ломаной на рис. 9.14 равна:
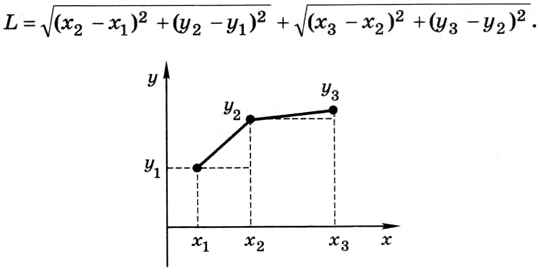
Рис. 9.14
Используя эту идею, разделим кривую линию на небольшие участки и заменим каждый участок отрезком так, чтобы получилась ломаная (штриховая линия на рис. 9.15).
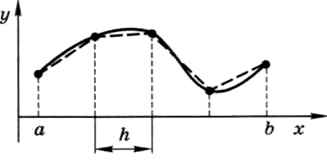
Рис. 9.15
Обычно разбивают исходный отрезок [а, 6] (на котором нужно определить длину кривой) на равные участки длины h. Конечно, длина ломаной отличается от длины кривой, но естественно предположить, что при уменьшении шага разбиения h эта разница будет уменьшаться.
Обратим внимание, что мы фактически выполнили дискретизацию — представили кривую в виде набора точек, при этом информация о поведении функции между этими точками была потеряна (вспомните оцифровку звука!). Величина h называется шагом дискретизации.
Подведём итоги:
• дискретизация позволяет представить задачу в виде, пригодном для компьютерных расчётов;
• при дискретизации часть информации теряется, поэтому все методы, основанные на дискретизации, — приближённые, они решают задачу с некоторой погрешностью;
• чтобы уменьшить погрешность, нужно уменьшать шаг дискретизации (увеличивать количество точек), но при этом возрастёт объём (и время) расчётов;
• при выборе малого шага дискретизации на результат могут сильно влиять погрешности вычислений, вызванные неточностью представления вещественных чисел в памяти компьютера (см. § 29).
Теперь можно составить программу. Будем считать, что константы (или переменные) а, b и h задают границы отрезка и шаг дискретизации. Тогда основная часть программы может выглядеть так на школьном алгоритмическом языке:

Возвращаясь к задаче с шариком, вспомним, что его движение описывается уравнениями:
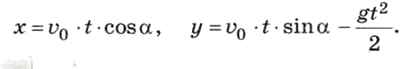
Если выразить время из первого уравнения и подставить во второе, получается
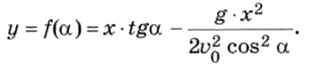
Это и есть функция, график которой нас интересует. Написать полную программу вы уже можете самостоятельно. Проверьте её работу для разных значений исходных данных (скорости и угла вылета, расстояния).
Следующая страница  Вычисление площадей фигур
Вычисление площадей фигур

