Уроки 115 - 116
Дискретизация. Вычисление длины кривой и площадей фигур
§71. Дискретизация

Содержание урока

Вычисление длины кривой

Вычисление площадей фигур

Вопросы и задания

Задачи

Вычисление площадей фигур

Применим метод дискретизации в другой достаточно сложной задаче — для вычисления площади фигуры. Пусть фигура, площадь которой нас интересует, ограничена графиками функций y = f₁(х) и y = f₂(х) (рис. 9.16).

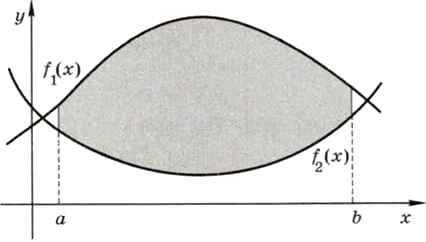
Рис. 9.16

В некоторых простых случаях (но далеко не всегда!) площадь такой фигуры можно вычислить аналитически с помощью методов высшей математики. Мы же будем использовать приближённые методы, применять которые значительно проще.

Как и при вычислении длины кривой, применим дискретизацию — разделим фигуру на отдельные полоски и заменим каждую полоску на другую фигуру, для которой мы можем легко найти площадь, например на прямоугольник (рис. 9.17).

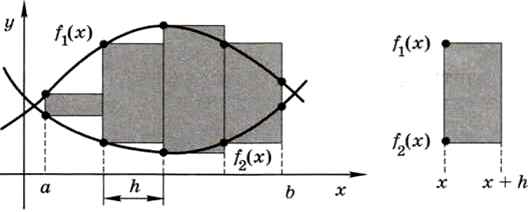
Рис. 9.17

Понятно, что площадь исходной фигуры в общем случае не совпадает с суммой площадей получившихся прямоугольников. Так и должно было быть, ведь при дискретизации информация о поведении функций между точками отсчёта была утеряна. Однако при уменьшении шага дискретизации h эта разница будет уменьшаться.

На рисунке 9.17 высота прямоугольника рассчитывается как разность значений функций на левой границе отрезка (можно использовать и правую границу). На практике обычно вычисляют высоту в середине отрезка (в точке х + h/2), тогда площадь прямоугольника будет более близка к площади полосы исходной фигуры. Заметим, что ширина каждого из прямоугольников равна h, поэтому в программе умножение на h можно выполнить в конце цикла:

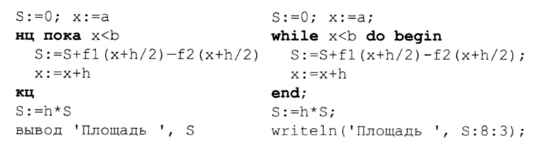
Этот метод называется методом прямоугольников.

Вместо прямоугольника для замены удобно применять ещё одну известную фигуру, для которой легко считается площадь, — трапецию (рис. 9.18).

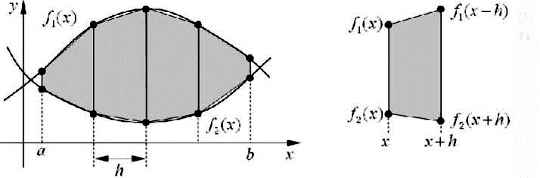
Рис. 9.18

Площадь трапеции равна произведению полусуммы её оснований на высоту, т. е. для элементарной трапеции с левой границей в точке х получаем выражение для площади:

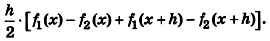
Простейшая программа выглядит так:

Этот метод называется методом трапеций.

Заметим, что правое основание очередной трапеции совпадает с левым основанием следующей, поэтому можно немного изменить программу, чтобы на каждом шаге цикла вычислялась разность функций только в одной точке. Сделайте это самостоятельно.

Следующая страница Вопросы и задания

Cкачать материалы урока