Уроки 115 - 116
Дискретизация. Вычисление длины кривой и площадей фигур
§71. Дискретизация

Содержание урока

Вычисление длины кривой

Вычисление площадей фигур

Вопросы и задания

Задачи

Задачи

1. Измените программу для вычисления длины кривой так, чтобы на каждом шаге цикла вычислять только одно значение функции.

2. Найдите приближённо длину параболы у = х² на отрезке х е[0, 10].

3. Для примера, разобранного в § 70, вычислите длину траектории движения шарика для углов вылета 35,5° и 65,8°. Сравните полученные результаты. Постройте эти траектории с помощью табличного процессора.

4. Решите задачу 3 при разных значениях шага. Какой шаг вы рекомендуете выбрать для этого случая? Почему?

5. В чём заключается дискретизация при вычислении площади?

*6. Измените программу для вычисления площади методом трапеций так, чтобы повторно не вычислять одни и те же величины.

7. Найдите площадь фигуры, ограниченной параболой у = х² и осью ОХ, на отрезке х е [0, 10].

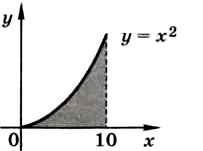
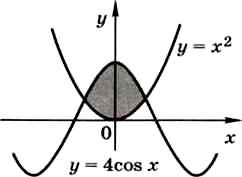
8. Найдите площадь фигуры, ограниченной графиками функций у = х² и у = 4сos х.

*9. Найдите площадь фигуры, ограниченной эллипсом

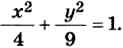
*10. Найдите с помощью приближённых методов площадь круга радиуса R = 2. Используя это значение, из формулы S = πR² определите приближенно число π.

Следующая страница §71. Дискретизация

Cкачать материалы урока