Уроки 117 - 118
Оптимизация с помощью табличных процессоров
§72. Оптимизация
Содержание урока
Локальные и глобальный минимумы
Пример: оптимальная раскройка листа
Использование табличных процессоров
Локальные и глобальный минимумы
По традиции в теории оптимизации рассматривают задачу поиска минимума. Если нужно найти максимум, просто меняют знак функции: значение функции f(x) максимально там, где значение функции (-fх)) минимально.
В математике различают локальный («местный») и глобальный («общий») минимумы. В точках х1, х2 и х3 функция, график которой показан на рис. 9.19, имеет локальные минимумы, это значит, что слева и справа от этих точек функция возрастает.
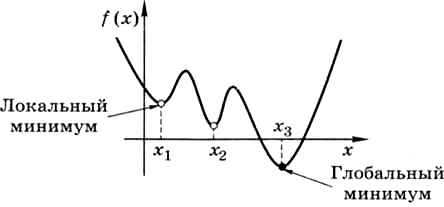
Рис. 9.19
Минимум в точке x3 — глобальный, потому что здесь функция имеет наименьшее значение во всей рассматриваемой области.
Очевидно, что нас всегда интересует глобальный минимум. Однако большинство существующих методов оптимизации предназначено именно для поиска локальных минимумов 1 вблизи заданной начальной точки (начального приближения). Можно представить себе, что график функции — это срез поверхности, на которую устанавливается шарик в некоторой начальной точке; куда этот шарик скатится, такой минимум и будет найден.
1 Для некоторых типов функций существуют методы глобальной оптимизации, но они сложны и выходят за рамки школьного курса.
Результат локальной оптимизации зависит от выбранного начального приближения.
Следующая страница 
Метод дихотомии
Cкачать материалы урока
