Уроки 15 - 16
Другие системы счисления
§14. Другие системы счисления
Содержание урока
§14. Другие системы счисления
Троичная уравновешенная система счисления
Двоично-десятичная система счисления
Троичная уравновешенная система счисления
В истории компьютерной техники применялись и другие системы счисления. Например, в 1958 г. была создана электронная вычислительная машина (ЭВМ) «Сетунь» (главный конструктор — Н. П. Брусенцов), которая использовала троичную систему счисления. Всего в 1960-х гг. было выпущено более 50 промышленных образцов ЭВМ «Сетунь».
В троичной уравновешенной системе основание равно 3, используются три цифры: 1 («минус 1»), 0 и 1. Один троичный разряд называется тритом (в отличие от двоичного бита). Система называется уравновешенной, потому что с помощью любого числа разрядов можно закодировать равное число положительных и отрицательных чисел, и число ноль. В таблице 2.7 показаны, например, все двухразрядные числа.
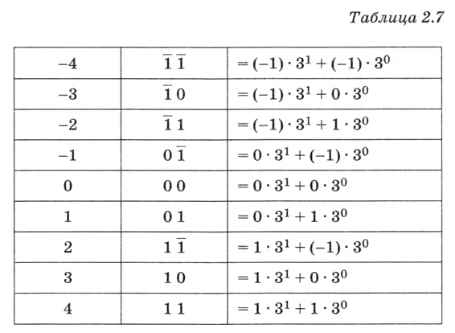
В последнем столбце этой таблицы числа записаны в развёрнутой форме, которую можно использовать для перевода из троичной уравновешенной системы в десятичную.
Заметьте, что положительные и отрицательные числа кодируются с помощью одних и тех же правил. Это большое преимущество по сравнению с двоичным кодированием, при котором для хранения отрицательных чисел пришлось изобретать специальный код.
Троичная уравновешенная система счисления даёт ключ к решению задачи Баше, которая была известна еще в XIII веке Леонардо Пизанскому (Фибоначчи):
Найти такой набор из 4 гирь, чтобы с их помощью на чашечках равноплечных весов можно было взвесить груз массой от 1 до 40 кг включительно. Гири можно располагать на любой чаше весов.
Каждая гиря может быть в трёх состояниях:
1) лежать на той же чаше весов, что и груз: в этом случае её вес вычитается из суммы (1);
2) не участвовать во взвешивании (0);
3) лежать на другой чаше: её вес добавляется к сумме (1).
Поэтому веса гирь нужно выбрать равными степеням числа 3, т. е. 1, 3, 9 и 27 кг.
Следующая страница  Двоично-десятичная система счисления
Двоично-десятичная система счисления

