Урок 26
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 1

Построение логического выражения. Способ 2

Построение логического выражения. Способ 3

Задачи

Построение логического выражения
Способ 1

До этого момента мы считали, что логическое выражение уже задано и нам надо что-то с ним сделать (построить таблицу истинности, упростить и т. п.). Такие задачи называются задачами анализа (от греческого — разложение), в них требуется исследовать заданное выражение. При проектировании различных логических устройств, в том числе и устройств компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греческого — совмещение).

В качестве простейшего примера построим логическое выражение, тождественное операции импликации X = А —> В, по её таблице истинности (рис. 3.19).

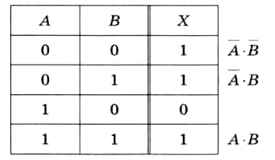
Рис. 3.19

Способ 1. В таблице истинности мы выделяем все строки, где логическое выражение равно единице. Тогда искомое выражение может быть записано как логическая сумма выражений, каждое из которых истинно только^ одном случае.

Например, выражение А • B истинно только при А = 0 и В = 0, т. е. только в первой строке таблицы. Выражение А • В истинно только во второй строке, а А • В — только в последней.

Существует простое правило: если в некоторой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.

Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем:

Х = А • B + А • В + А • В.

Упрощаем это выражение:

X = А • (B + В) + А • В = А + А • В = (А + А) • (А + В) = А + В.

Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ».

Следующая страница Построение логического выражения. Способ 2

Cкачать материалы урока