Урок 26
Синтез логических выражений
§22. Синтез логических выражений

Содержание урока

Построение логического выражения. Способ 1

Построение логического выражения. Способ 2

Построение логического выражения. Способ 3

Задачи

Построение логического выражения
Способ 2

Способ 2. Если в таблице истинности нулей меньше, чем единиц, удобнее сначала найти формулу для обратного выражения, X, а потом применить операцию «НЕ». В данном случае выражение равно нулю в единственной строке, при А =1 и В =0, только в этой строке X = 1, поэтому, используя предыдущий способ, получаем X = А • В. Теперь остаётся применить операцию «НЕ» и закон де Моргана:

Х = А • B = A + В.

Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 3.20).

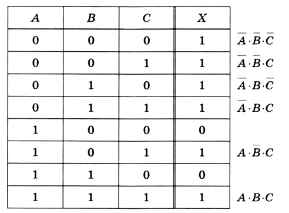
Рис. 3.20

Отметим все строки, где X = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20). Теперь выполним логическое сложение:

Х = А • B • C + А • B • C + А • B • C + А • B • C + А • B • C + А • B • C.

Упрощение этого выражения даёт:

X = А • B • (C + С) + А • В (C + С) + А • С • (B + В) = А • B + А • B + А • С = А • (B + В) + А • С = А + А • С = (А + А) • (А +С) = А + С.

Используя второй способ, получаем:

X = А • B • (C + А • В • C = А • C • (B + В) = А • C.

Тогда X = А • C = А + С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц.

Следующая страница Построение логического выражения. Способ 3

Cкачать материалы урока