Урок 29
Решение уравнений в табличных процессорах
§70. Решение уравнений

Содержание урока

Приближённые методы

Метод перебора

Метод деления отрезка пополам

Пример: полёт мяча

Использование табличных процессоров

Вопросы и задания

Задачи

Приближённые методы

На уроках математики вас учили искать решение уравнения в виде формулы, выражающей неизвестную величину через известные. Например, решение уравнения ах + b = 1 при а ≠ 0 можно записать в виде х = (1 - b)/а. Такое решение называется аналитическим, оно может быть использовано для теоретического исследования (изучения влияния исходных данных на результат).

Однако не все уравнения можно (на современном уровне развития математики) решить аналитически. Иногда решение есть, но очень сложное. Например, уравнение x = cosx так просто не решается. В этом случае приходится использовать другие методы решения, например графический: построить по точкам графики функций, стоящих в левой и правой частях равенства, и посмотреть, где они пересекаются (рис. 9.3). Затем решение можно уточнять, уменьшая шаг при построении графика до получения требуемой точности.

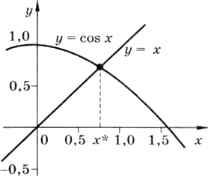
Рис. 9.3

Если нужна высокая точность, графический метод требует очень большого объёма вычислений, который имеет смысл поручить компьютеру. Однако нужно как-то учесть, что компьютер не способен «посмотреть» на график, и для уточнения решения может использовать только числовые данные. Компьютерный алгоритм решения уравнения может выглядеть примерно так:

1) выбрать отрезок [а0, b0] для поиска решения (обычно предполагается, что на этом отрезке решение есть, и притом только одно);
2) с помощью некоторого алгоритма уточнить решение, перейдя к меньшему отрезку [а, b];
3) повторять шаг 2, пока длина отрезка (содержащего решение) не станет достаточно мала.

Здесь не совсем ясно, что значит «пока длина отрезка не станет достаточно мала». Обычно задается нужная точность ε: это означает, что отклонение полученного решения от истинного х^* не должно быть больше ε. Если корень уравнения находится на отрезке [а, b], то в качестве решения лучше всего взять его середину (а+b)/2. В этом случае погрешность будет минимальной: не больше половины длины отрезка. Поэтому цикл нужно остановить, когда длина отрезка станет меньше, чем 2ε.

Часто используется другой вариант, когда отрезок не нужен, а требуется знать только одну точку вблизи решения:

1) выбрать начальное приближение х₀ около решения;
2) с помощью некоторого алгоритма перейти к следующему приближению х, которое находится ближе к точному решению х^*
3) повторять шаг 2, пока на очередном шаге решение не изменится на величину, меньшую, чем допустимая погрешность ε.

Подобные методы решения уравнений называются приближёнными. Их суть в том, что решение последовательно уточняется до тех пор, пока не будет найдено с требуемой точностью. Поскольку при каждом уточнении выполняются одинаковые действия, можно назвать такие методы итерационными (от лат. iteration — повторение).

Приближённые методы имеют ряд недостатков:

• получается приближённое решение, а не точное; это значит, что нельзя написать х^* = 1,2345, нужно использовать знак приближённого равенства: х^* ≈ 1,2345 (отметим ещё раз, что практически все вычисления с дробными числами на компьютере выполняются неточно);
• мы получаем не формулу, а число, по которому невозможно оценить, как меняется решение при изменении исходных данных (сложно выявить зависимость от параметра);
• объём вычислений может быть слишком велик, часто это не позволяет использовать приближённые методы в системах реального времени;
• не всегда можно оценить погрешность результата.

Однако в некоторых практических случаях приближённые методы более полезны, чем аналитические. Они обладают следующими достоинствами:

• часто получение аналитического решения невозможно или требует значительных усилий, тогда как приближенные методы позволяют достаточно быстро решить задачу с заданной точностью;
• при компьютерных расчётах (с конечной точностью) вычисления по «точным» аналитическим формулам часто могут давать очень неточный результат из-за вычислительной неустойчивости метода. Нередко для таких задач (например, для решения систем линейных уравнений) специально разрабатываются приближённые методы, которые дают значительно более точное решение.

Следующая страница Метод перебора

Cкачать материалы урока