Урок 29
Решение уравнений в табличных процессорах
§70. Решение уравнений

Содержание урока

Приближённые методы

Метод перебора

Метод деления отрезка пополам

Пример: полёт мяча

Использование табличных процессоров

Вопросы и задания

Задачи

Метод перебора

Как принято в вычислительной математике, далее мы будем рассматривать уравнение общего вида f(х) = 0, к которому можно привести любое заданное уравнение. Например, для уравнения х = cos х получаем f(x) = х - cos х.

Предположим, что нужно найти решение уравнения f(х) = 0 с точностью ε, причём известно (например, видно на графике), что решение находится справа от некоторой точки х = а. В этом случае можно разбить всю область, где может быть решение, на узкие полоски шириной δ = 2ε, и выбрать такую полоску, где график функции пересекает ось ОХ (рис. 9.4).

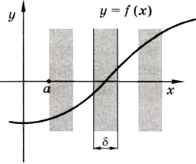
Рис. 9.4

Для того чтобы поручить решение этой задачи компьютеру, нужно ответить на два вопроса:

1) Как с помощью математических операций определить, что в полосе [х, х + δ] есть решение?
2) Что считать решением уравнения, когда такая полоса определена?

Проще ответить на второй вопрос: лучше всего взять в качестве решения середину полосы, т. е. точку х_* =х + ε (в этом случае погрешность будет не больше, чем ε).

Для того чтобы определить, есть ли решение на отрезке [х, х + δ], сравним значения функции на концах этого отрезка. Рассмотрим три случая, показанные на рис. 9.5, а-в.

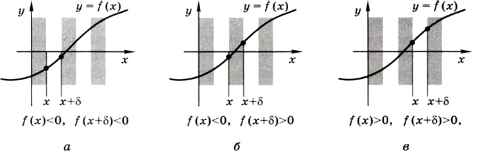
Рис. 9.5

Несложно понять, что если график пересекает ось ОХ, то на концах отрезка функция имеет разные знаки, т. е. f(х) • f/(х + δ) ≤ 0. При этом важно, чтобы график не имел разрывов.

Если непрерывная функция имеет разные знаки на концах отрезка [x₁, х₂], то в некоторой точке внутри этого отрезка она равна нулю.

Таким образом, нужно найти отрезок шириной 2е, на концах которого функция имеет разные знаки, и взять в качестве решения его середину. Решение этой задачи при а = 0 может выглядеть, например, так (слева приведена программа на школьном алгоритмическом языке, а справа — на языке Паскаль):

Здесь заданная точность ε хранится в виде константы eps, а вычисление функции f(x) оформлено в виде подпрограммы-функции f. Поиск решения начинается с нуля (в других задачах начальное значение может быть другим). Цикл останавливается, когда для очередного отрезка получаем f(x) • f(x + δ) ≤ 0.

Нужно понимать, что при вычислениях на реальном компьютере мы не можем задавать произвольно малое значение £. Точность ограничена типом данных, с помощью которого выполняются вычисления. В практических расчётах чаще всего используются данные с двойной точностью (англ, double), для которых предельная точность близка к 10^-16 (вспомните материал § 26 и 29).

Обратите внимание, что в этом простейшем варианте программа зациклится, если справа от нуля решения нет. Подумайте, как изменить программу так, чтобы зацикливания не было.

Кроме того, в приведённом алгоритме есть и ещё одна возможная неточность: подумайте, что случится, если случайно получится f(x) = 0 или /(х + δ) = 0. Поскольку условие цикла при этом нарушается, цикл закончится, и будет получен результат с требуемой точностью Е. Однако в этом случае можно было бы определить решение более точно, что вам и предлагается сделать самостоятельно.

Главный недостаток метода перебора — большое количество операций. Например, для решения уравнения с точностью 0,001 может понадобиться несколько тысяч вычислений значения функции f(х). Поэтому сначала можно использовать перебор с достаточно большим шагом, чтобы отделить корни, т. е. найти интервалы, в каждом из которых есть только один корень. После этого выполняется уточнение корней — перебор внутри каждого из таких интервалов с шагом δ = 2ε, достаточным для определения решения с заданной точностью.

Следующая страница Метод деления отрезка пополам

Cкачать материалы урока