Урок 29
Решение уравнений в табличных процессорах
§70. Решение уравнений

Содержание урока

Приближённые методы

Метод перебора

Метод деления отрезка пополам

Пример: полёт мяча

Использование табличных процессоров

Вопросы и задания

Задачи

Использование табличных процессоров

Для численного решения уравнений можно использовать табличный процессор, например OpenOffice.org Calc (или LibreOffice Calc) или Microsoft Excel. Обычно сначала строится график функции, который позволяет определить количество решений уравнения и их примерное расположение; затем используется модуль «Поиск решения». Далее мы будем рассматривать программу Calc из пакета OpenOffice.org, указывая на незначительные отличия Excel.

Введём исходные данные для рассмотренной задачи бросания мяча, как показано на рис. 9.8. Для того чтобы формулы выглядели более привычно, дадим ячейкам Bl, В2 и В3 имена S, Н и v (их можно ввести в левом верхнем углу таблицы).

В столбце А заполним ряд значений углов от 0^o до 85^o с шагом 5^o. Для этого введём два первых значения, выделим эти ячейки и «растянем» за маркер заполнения (квадратик в правом нижнем углу выделенной части, рис. 9.9).

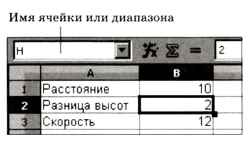
Рис. 9.8

Рис. 9.9

Добавим столбцы, в которых для каждого угла будут вычисляться его значение в радианах (с помощью стандартной функции RADIANS, в русской версии Excel — РАДИАНЫ), время полёта, координата у и значение функции f(а) (рис. 9.10).

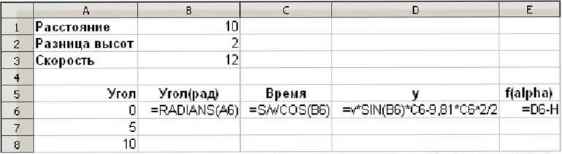
Рис. 9.10

Обратите внимание, что в формулах мы используем имена ячеек S, Н и v. Это абсолютные ссылки, не меняющиеся при копировании; например, вместо имени S можно было бы написать адрес $В$1, но это было бы менее понятно. Эти формулы можно просто «растянуть» (скопировать) вниз за маркер заполнения.

Теперь построим график функции f(а). Сначала нужно выделить данные в столбцах А и Е, это можно сделать, если удерживать нажатой клавишу Ctrl. Затем строим диаграмму типа Диаграмма XY (в Excel — диаграмма Точечная) — рис. 9.11. График функции пересекает ось ОХ в двух точках, т. е. уравнение f(а) = 0 имеет два решения, одно около 35^o, второе — около 65^o.

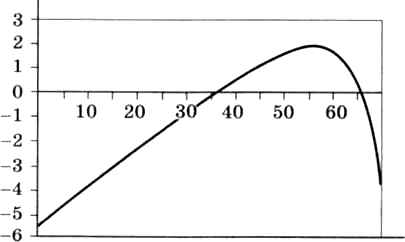
Рис. 9.11

Теперь уточним решение, используя возможности табличного процессора, в котором реализован один из приближённых методов решения уравнений. Для этого нужно знать начальное приближение α₀ — значение неизвестной величины, достаточно близкое к решению. По графику мы определили, что первый раз график пересекает ось ОХ для значения угла около 35^o, поэтому можно взять α₀ = 35^o. Запишем это значение в свободную ячейку, например в Н2, и добавим недостающие формулы так, чтобы получить значение функции f(а) в ячейке L2 (рис. 9.12).

Рис. 9.12

Задача подбора параметра формулируется так: «установить в ячейке ... значение ..., изменяя значение ячейки ...». Например, в нашем случае нужно установить в ячейке L2 значение 0, изменяя Н2. Ячейка L2 называется целевой, потому что наша цель — получить в ней определённое значение (ноль). Ячейка Н2 — это изменяемая ячейка. В главном меню выбираем пункт Сервис, Подбор параметра и вводим эти данные (рис. 9.13).

Рис. 9.13

После нажатия на кнопку ОК найденное решение уравнения будет записано в ячейку Н2.

Как же найти второе решение? Для этого нужно выбрать другое начальное приближение, например α₀ = 70^o, в остальном порядок действий не меняется. Сделайте это самостоятельно.

Проверьте, что будет происходить при изменении начальной скорости до 10 м/с и до 20 м/с. Попробуйте объяснить эти результаты с точки зрения физики.

Следующая страница Вопросы и задания

Cкачать материалы урока