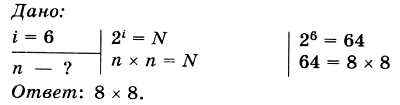Урок 2
§2. Подходы к измерению информации

2.1. Содержательный подход к измерению информации

Клод Шеннон, разрабатывая теорию связи, предложил характеризовать информативность сообщения содержащейся в нём полезной информацией, т. е. той частью сообщения, которая снимает полностью или уменьшает существующую до её получения неопределённость какой-либо ситуации.

Клод Элвуд Шеннон (1916-2001) — американский инженер и математик. Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи. В 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы информации.

Информация — это снятая неопределённость. Величина неопределённости некоторого события — это количество возможных результатов (исходов) данного события.

Сообщение, уменьшающее неопределённость знания в 2 раза, несёт 1 бит информации.

Такой подход к измерению информации называют содержательным.

Пример 1. Допустим, вы подбрасываете монету, загадывая, что выпадет: «орёл» или «решка». Перед подбрасыванием монеты неопределённость знания о результате равна двум. Действительно, есть всего два возможных результата этого события (бросания монеты). Эти результаты мы считаем равновероятными, т. к. ни один из них не имеет преимущества перед другим.

После того как конкретный исход стал известен (например, подброшенная монета упала «орлом» вверх), неопределённость уменьшилась в 2 раза. Таким образом, сообщение о том, что подброшенная монета упала «орлом» вверх, несёт в себе 1 бит информации.

Пример 2. Предположим, в книжном шкафу восемь полок. Книга может быть поставлена на любую из них. Сколько бит информации несёт сообщение о том, что книга поставлена на третью полку?

Ответ на этот вопрос можно получить, если дополнить исходное сообщение ещё несколькими сообщениями так, чтобы каждое из них уменьшало неопределённость знания в 2 раза.

Итак, количество возможных результатов (исходов) события, состоящего в том, что книга поставлена в шкаф, равно восьми: 1, 2, 3, 4, 5, 6, 7 и 8.

Сообщение «Книга поставлена на полку не выше четвёртой» уменьшает неопределённость знания о результате в два раза. Действительно, после такого сообщения остаётся всего четыре варианта: 1, 2, 3 и 4. Получен один бит информации.

Сообщение «Книга поставлена на полку выше второй» уменьшает неопределённость знания о результате в два раза: после этого сообщения остаётся всего два варианта: 3 и 4. Получен ещё один (второй) бит информации.

Сообщение «Книга поставлена на третью полку» также уменьшает неопределённость знания о результате в два раза. Получен третий бит информации.

Итак, мы построили цепочку сообщений, каждое из которых уменьшало неопределённость знания о результате в два раза, т. е. несло 1 бит информации. Всего было набрано 3 бита информации. Именно столько информации и содержится в сообщении «Книга поставлена на третью полку».

Подумайте, сколько информации содержится в сообщении о том, что книга поставлена на пятую полку. Обоснуйте свой ответ, построив соответствующую цепочку сообщений.

Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется методом половинного деления. Этот метод широко используется в компьютерных науках.

Пример 3. О результатах футбольного матча между клубами «Спартак» и «Динамо» известно, что больше трёх мячей никто не забил. Всего возможных вариантов счёта матча — 16:

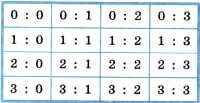
Здесь первая цифра в каждой паре соответствует количеству мячей, забитых командой «Спартак», вторая — командой «Динамо».

Будем считать все варианты равновероятными и отгадывать счёт, задавая вопросы, на которые можно ответить только «да» или «нет». Вопросы будем формулировать так, чтобы количество возможных вариантов счёта каждый раз уменьшалось вдвое. Это позволит нам:

1) обойтись минимальным количеством вопросов;

2) подсчитать, сколько бит информации содержит сообщение о счёте матча.

Вопрос 1. «Спартак» забил больше одного мяча? Предположим, получен ответ «Нет». Такой ответ позволяет не рассматривать варианты, расположенные в нижней части таблицы, т. е. сокращает количество возможных исходов в 2 раза:

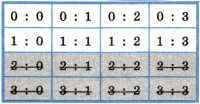
Вопрос 2. «Спартак» забил один мяч? Предположим, получен ответ «Да». Такой ответ позволяет не рассматривать варианты, расположенные в верхней строке таблицы, т. е. сокращает количество возможных исходов ещё в 2 раза:

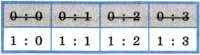
Вопрос 3. «Спартак» пропустил больше одного мяча? Предположим, получен ответ «Нет». Можно отбросить ещё два варианта:

Вопрос 4. «Спартак» пропустил один мяч? Предположим, получен ответ «Да». Получаем единственный вариант:

Итак, нам удалось выяснить счёт матча, задав четыре вопроса, ответ на каждый из которых уменьшал неопределённость результата в два раза, т. е. нёс 1 бит информации. Сообщение о счёте матча несёт четыре бита информации.

Выясните, какому счёту матча будут соответствовать следующие цепочки ответов на поставленные выше вопросы:

1) Да - Да - Да - Да;

2) Нет - Нет - Нет - Нет;

3) Да - Нет - Да - Нет.

Попробуйте придумать такие вопросы, чтобы цепочка ответов Нет - Да - Нет - Да приводила к счёту 2 : 3.

Вычислять количество информации, содержащееся в сообщении о том, что имел место один из множества равновероятных результатов некоторого события, с помощью метода половинного деления возможно, но затруднительно. Гораздо проще воспользоваться следующей закономерностью.

Количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы: 2ⁱ = N.

При N, равном целой степени двойки (2, 4, 8, 16, 32 и т. д.), это уравнение легко решается в уме. Решать такие уравнения при других N вы научитесь чуть позже, в курсе математики 11 класса.

Примюр 4. Петя и Вася заинтересовались игрой «Крестики - нолики» на поле n х n. Количество информации, полученное вторым игроком после первого хода первого игрока, составляет б бит. Требуется выяснить размеры поля, на котором играют Петя и Вася.

Cкачать материалы урока