Урок 2
§2. Подходы к измерению информации

2.2. Алфавитный подход к измерению информации

Определение количества информации на основе уменьшения неопределённости наших знаний рассматривает информацию с точки зрения её содержания, понятности и новизны для человека. С этой точки зрения в примере о подбрасывании монеты одинаковое количество информации содержит и зрительный образ упавшей монеты, и короткое сообщение «Орёл», и длинная фраза «В результате подбрасывания монета упала так, что на её видимой части изображён орёл».

Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от её содержания и рассматривать информацию как последовательность символов (букв, цифр, кодов цвета точек изображения и т. д.) некоторого алфавита.

Информация — последовательность символов (букв, цифр, кодов цвета точек изображения и т. д.) некоторого алфавита.

Минимальная мощность алфавита (количество входящих в него символов), пригодного для кодирования информации, равна 2. Такой алфавит называется двоичным. Один символ двоичного алфавита несёт 1 бит информации.

Согласно Колмогорову, количество информации, содержащейся в последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этой последовательности, безотносительно к содержанию представленного ею сообщения. Данный подход к определению количества информации называют алфавитным.

Андрей Николаевич Колмогоров (1903-1987) — один из крупнейших математиков XX века. Им получены основополагающие результаты в математической логике, теории сложности алгоритмов, теории информации, теории множеств и ряде других областей математики и её приложений.

Информационным объёмом сообщения называется количество двоичных символов, которое используется для кодирования этого сообщения. В двоичном коде один двоичный разряд несёт 1 бит информации.

В отличие от определения количества информации по Колмогорову в определении информационного объёма не требуется, чтобы число двоичных символов было минимально возможным. При оптимальном кодировании понятия количества информации и информационного объёма совпадают.

Из курса информатики основной школы вы знаете, что двоичные коды бывают равномерные и неравномерные. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные — разное.

Первый равномерный двоичный код был изобретён французом Жаном Морисом Бодо в 1870 году. В коде Бодо используются сигналы двух видов, имеющие одинаковую длительность и абсолютную величину, но разную полярность. Длина кодов всех символов алфавита равна пяти (рис. 1.7).

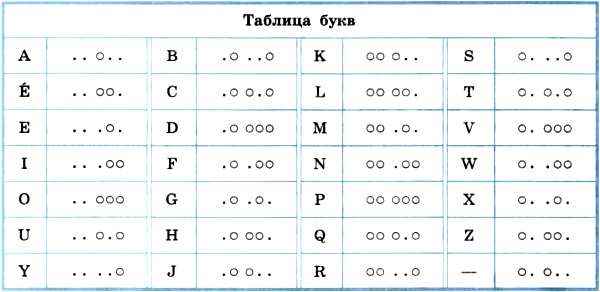
Рис. 1.7. Фрагмент кодовой таблицы кода Бодо

Всего с помощью кода Бодо можно составить 2⁵ = 32 комбинации.

Пример 5. Слово WORD, закодированное с помощью кода Бодо, будет выглядеть так:

Информационный объём такого сообщения равен 20 битам; таково количество двоичных символов, которое используется для кодирования этого сообщения.

Пример 6. Для двоичного представления текстов в компьютере чаще всего используется равномерный восьмиразрядный код. С его помощью можно закодировать алфавит из 256 символов (2⁸ = 256). Фрагмент кодовой таблицы ASCII представлен на рисунке 1.8.

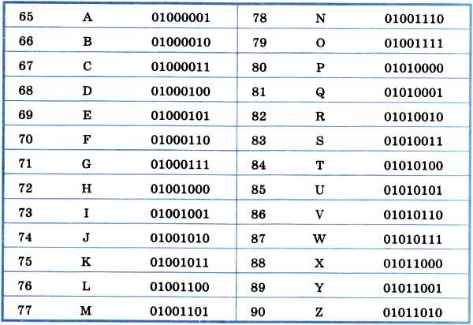
Рис. 1.8. Фрагмент кодовой таблицы ASCII

Слово WORD, закодированное с помощью таблицы ASCII:

Информационный объём такого сообщения равен 32 битам.

Из курса информатики основной школы вам известно, что с помощью i-разрядного двоичного кода можно закодировать алфавит, мощность N которого определяется из соотношения:

2ⁱ = N.

Иными словами, зная мощность используемого алфавита, всегда можно вычислить информационный вес символа — минимально возможное количество бит, требуемое для кодирования символов этого алфавита. При этом информационный вес символа должен быть выражен целым числом.

Соотношение для определения информационного веса символа алфавита можно получить и из следующих соображений.

Пусть N — мощность алфавита, используемого для кодирования сообщений. При этом в каждом конкретном сообщении какие-то символы алфавита будут использоваться чаще, какие-то — реже, а какие-то — не будут использоваться вообще. Не станем обращать на это внимание, наоборот, будем считать, что любой из символов может появиться в сообщении с равной вероятностью. Другими словами, появление в сообщении очередного символа — одно из N равновероятных событий. Но количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы 2ⁱ = N.

Алгоритм вычисления информационного объёма сообщения выглядит так:

1) определить мощность используемого алфавита N;

2) из соотношения 2ⁱ = N определить i — информационный вес символа алфавита в битах (длину двоичного кода символа из используемого алфавита мощности N);

3) вычислить информационный объём сообщения I, умножив информационный вес символа i на количество символов в сообщении К.

При алфавитном подходе информационный объём сообщения I, состоящего из К символов, вычисляется по формуле:

I = К * i,

где I — информационный вес символа в битах, связанный с мощностью используемого алфавита N соотношением:

2ⁱ = N.

Пример 7. Для регистрации на некотором сайте пользователю надо придумать пароль, состоящий из 10 символов. В качестве символов можно использовать десятичные цифры и шесть первых букв латинского алфавита, причём буквы используются только заглавные. Пароли кодируются посимвольно. Все символы кодируются одинаковым и минимально возможным количеством бит. Для хранения сведений о каждом пользователе в системе отведено одинаковое и минимально возможное целое число байт.

Необходимо выяснить, какой объём памяти потребуется для хранения 100 паролей.

Cкачать материалы урока