Урок 2
§2. Подходы к измерению информации

2.3. Единицы измерения информации

Итак, в двоичном коде один двоичный разряд несёт 1 бит информации. 8 бит образуют один байт. Помимо бита и байта, для измерения информации используются более крупные единицы:

1 Кбайт (килобайт) = 2¹⁰ байт;

1 Мбайт (мегабайт) = 2¹⁰ Кбайт = 2²⁰ байт;

1 Гбайт (гигабайт) = 2¹⁰ Мбайт = 2²⁰ Кбайт = 2³⁰ байт;

1 Тбайт (терабайт) = 2¹⁰ Гбайт = 2²⁰ Мбайт = 2³⁰ Кбайт = 2⁴⁰ байт;

1 Пбайт (петабайт) = 2¹⁰ Тбайт = 2²⁰ Гбайт = 2³⁰ Мбайт = 2⁴⁰ Кбайт = 2⁵⁰ байт.

Исторически сложилось так, что приставки «кило», «мега», «гига», «тера» и др. в информатике трактуются не так, как в математике, где «кило» соответствует 10³, «мега» — 10⁶, «гига» — 10⁹, «тера» — 10¹² и т. д.

Это произошло потому, что 2¹⁰ = 1024 ≈ 1000 = 10³. Поэтому 1024 байта и стали называть килобайтом, 2¹⁰ килобайта стали называть мегабайтом и т. д.

Чтобы избежать путаницы с различным использованием одних и тех же приставок, в 1999 г. Международная электротехническая комиссия ввела новый стандарт наименования двоичных приставок. Согласно этому стандарту, 1 килобайт равняется 1000 байт, а величина 1024 байта получила новое название — 1 кибибайт (Кибайт).

У нас в стране в 2009 году принято «Положение о единицах величин, допускаемых к применению в Российской Федерации». В нём сказано, что наименование и обозначение единицы количества информации «байт» (1 байт = 8 бит) применяются с двоичными приставками «кило», «мега», «гига», которые соответствуют множителям «2¹⁰», «2²⁰» и «2³⁰» (1 Кбайт = 1024 байт, 1 Мбайт = 1024 Кбайт, 1 Гбайт = 1024 Мбайт). Данные приставки пишутся с большой буквы.

Рассмотрим ещё несколько примеров решения задач, связанных с определением информационного объёма сообщений.

Пример 8. При регистрации в компьютерной системе каждому пользователю выдаётся пароль длиной в 12 символов, образованный из десятичных цифр и первых шести букв английского алфавита, причём буквы могут использоваться как строчные, так и прописные — соответствующие символы считаются разными. Пароли кодируются посимвольно. Все символы кодируются одинаковым и минимально возможным количеством бит. Для хранения сведений о каждом пользователе в системе отведено одинаковое и минимально возможное целое число байт.

Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, для которых отведено 12 байт. На какое максимальное количество пользователей рассчитана система, если для хранения сведений о пользователях в ней отведено 200 Кбайт?

Прежде всего, выясним мощность алфавита, используемого для записи паролей: N — 6 (буквы прописные) + 6 (буквы строчные) + 10 (десятичные цифры) = 22 символа.

Для кодирования одного из 22 символов требуется 5 бит памяти (4 бита позволят закодировать всего 2⁴ = 16 символов, 5 бит позволят закодировать уже 2⁵ = 32 символа); 5 — минимально возможное количество бит для кодирования 22 разных символов алфавита, используемого для записи паролей.

Для хранения всех 12 символов пароля требуется 12 • 5 = 60 бит. Из условия следует, что пароль должен занимать целое число байт; т. к. 60 не кратно восьми, возьмём ближайшее большее значение, которое кратно восьми: 64 = 8 • 8. Таким образом, один пароль занимает 8 байт.

Информация о пользователе занимает 20 байт, т. к. содержит не только пароль (8 байт), но и дополнительные сведения (12 байт).

Максимальное количество пользователей («польз.»), информацию о которых можно сохранить в системе, равно 10 240:

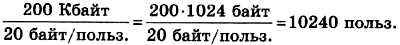
Пример 9. Объём сообщения, состоящего из 8192 символов, равен 16 Кбайт. Какова максимальная мощность алфавита, использованного при передаче сообщения?

Cкачать материалы урока