Урок 13
§11.1-11.4. Перевод чисел из одной позиционной системы счисления в другую

11.1. Перевод целого десятичного числа в систему счисления с основанием q

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Рассмотрим примеры перевода целых десятичных чисел в 2-ичную, 8-ричную и 16-ричную системы счисления.

Пример 1.

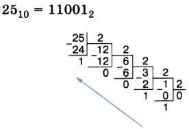
Пример 2.

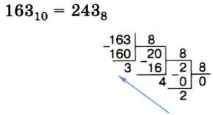
Пример 3.

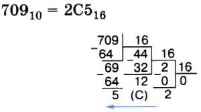
Пример 4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 22 оканчивается на 4.

Поскольку запись числа в системе счисления с основанием q заканчивается на 4, остаток от деления числа 22 на q равен 4: 22 mod q = 4¹⁾. Следовательно, 18 mod q = 0. Это верно для q ∈ {18, 9, 6, 3, 2, 1}.

---

¹⁾ Операция mod — вычисление остатка от целочисленного деления.

Так как в новой системе счисления запись числа оканчивается на 4, то q > 4. Следовательно, условию задачи удовлетворяют основания: 18, 9 и 6.

Cкачать материалы урока