Урок 13
§11.1-11.4. Перевод чисел из одной позиционной системы счисления в другую

11.3. Перевод целого числа из системы счисления с основанием р в систему счисления с основанием q

Каждый из нас может выполнять арифметические операции в привычной десятичной системе счисления. Выполнять такие же операции в других системах счисления человеку непривычно, а поэтому и неудобно.

Для того чтобы перевести целое число из системы счисления с основанием р в систему счисления с основанием q, достаточно:

1) основание новой системы счисления выразить в исходной системе счисления и все последующие действия производить в исходной системе счисления;
2) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
4) составить число в новой системе счисления, записывая его, начиная с последнего остатка.

При необходимости перевести целое число из системы счисления с основанием р в систему счисления с основанием q можно попытаться воспользоваться описанным выше алгоритмом. Другой способ состоит в том, чтобы свести всё к хорошо знакомым действиям в десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления (рис. 3.3).

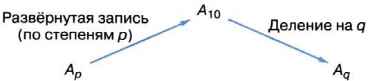
Рис. 3.3. Схема перевода целого числа из системы счисления с основанием р
в систему счисления с основанием q через десятичную систему счисления

Пример 5.

1234₅ = 1 • 5³ + 2 • 5² + 3 • 5¹ + 4 • 5⁰ = 194₁₀ = 522₆.

Cкачать материалы урока