Урок 15
§12. Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

В начальной школе для обучения детей счёту используют таблицы сложения и умножения. Подобные таблицы можно составить для любой позиционной системы счисления.

12.1. Сложение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц сложения в троичной (табл. 3.2), восьмеричной (табл. 3.4) и шестнадцатеричной (табл. 3.3) системах счисления.

Таблица 3.2

Сложение в троичной системе счисления

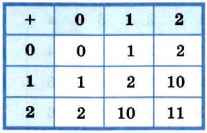
Таблица 3.3

Сложение в шестнадцатеричной системе счисления

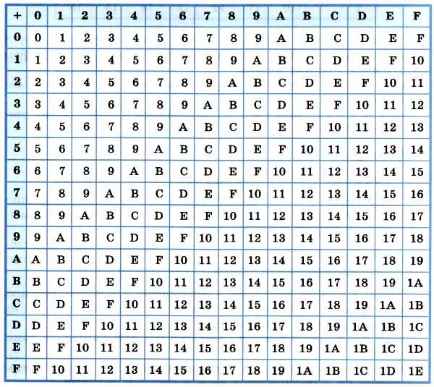
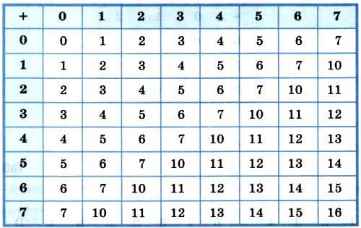
Таблица 3.4

Сложение в восьмеричной системе счисления

Чтобы в системе счисления с основанием q получить сумму S двух чисел А и Б, надо просуммировать образующие их цифры по разрядам i справа налево:

• если a_i + b_i < q, то s_i = a_i + b_i, старший (i + 1)-й разряд не изменяется;
• если a_i + b_i ≥ q, то s_i = а_i + b_i - q, старший (i + 1)-й разряд увеличивается на 1.

Примеры:

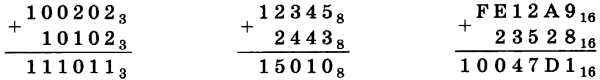
12.2. Вычитание чисел в системе счисления с основанием q

Чтобы в системе счисления с основанием q получить разность R двух чисел А и В, надо вычислить разности образующих их цифр по разрядам i справа налево:

• если a_i ≥ b_i , то r_i = a_i - b_i, старший (i + 1)-й разряд не изменяется;
• если a_i < b_i , то r_i = a_i - b_i + g, старший (i + 1)-й разряд уменьшается на 1 (выполняется заём в старшем разряде).

Примеры:

Cкачать материалы урока