Урок 15
§12. Арифметические операции в позиционных системах счисления

12.3. Умножение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц умножения в троичной (табл. 3.5), восьмеричной (табл. 3.6) и шестнадцатеричной (табл. 3.7) системах счисления.

Таблица 3.5

Умножение в троичной системе счисления

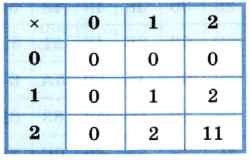
Таблица 3.6

Умножение в восьмеричной системе счисления

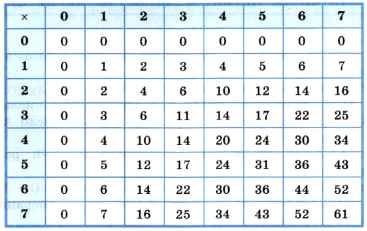
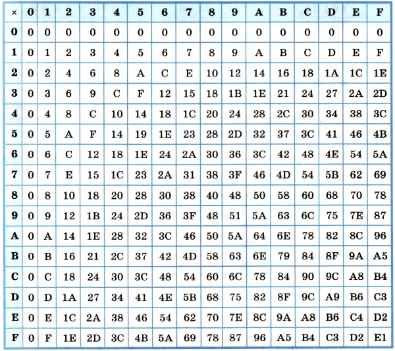
Таблица 3.7

Умножение в шестнадцатеричной системе счисления

Рассмотрим алгоритм умножения многозначного числа на однозначное.

Чтобы в системе счисления с основанием q получить произведение М многозначного числа А и однозначного числа b, надо вычислить произведения b и цифр, образующих число А по разрядам i справа налево:

• если a_i • b < q, то m_i = a_i • b, старший (i + 1)-й разряд не изменяется;
• если а_i • b ≥ q, то m_i = а_i • b mod q, старший (i + 1)-й разряд увеличивается на a_i • b div q (где div — операция целочисленного деления).

Примеры:

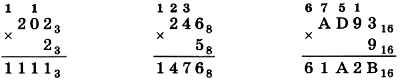
Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы в одном столбце оказались их самые младшие разряды с цифрами, отличными от нуля. Нули переносятся в итоговое произведение, а в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат.

Примеры:

Cкачать материалы урока