Урок 22
§18. Алгебра логики

Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.

18.1. Логические высказывания и переменные

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно.

Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.

Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?

Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если ..., то», «тогда и только тогда» и др.

Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).

Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем В, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и В». Здесь А, В — логические переменные, «и» — логическая связка.

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».

Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:

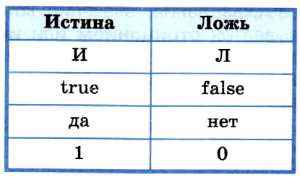
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Cкачать материалы урока