Урок 22
§18. Алгебра логики

18.4. Предикаты и их множества истинности

Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х < 12 становится истинным высказыванием при х = 5 (5 < 12 — истина) и ложным при x: = 15 (15 < 12 — ложь). Предложения такого рода называют высказывательными формами или предикатами.

Предикат — это утверждение, содержащее одну или несколько переменных.

Выделим некоторый предикат Р(х) и рассмотрим множество всевозможных объектов I, к которым он относится, — область определения предиката. Можно выделить такое подмножество Р множества I, что на всех его элементах предикат Р(х) будет превращаться в истинное высказывание. Определённое таким образом Р называется множеством истинности предиката Р(х).

Рассмотрим множество учеников некоторого класса. Известно, что в этом классе два отличника — Иван и Саша. Предикат «Он отличник» будет истинным высказыванием только по отношению к этим двум ученикам и ложным по отношению ко всем остальным.

Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката Р(х) = (х < 0) — множество отрицательных чисел; множество истинности предиката Р(х, у) = (х² + у² = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x² — 3x + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (x² — 3x + 2 = 0).

Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ∨ В(х).

Пример 5. Найдём все целые числа 2, превращающие предикат

P(z) = (z > 5) & (z — 2 < 15) в

истинное высказывание. Другими словами, требуется найти множество истинности предиката P(z), заданного на множестве целых чисел I.

Предикат P(z) состоит из двух предикатов, соединённых операцией конъюнкции: P(z) = A(z) & B(z). Рассмотрим каждый из них в отдельности.

Множеством истинности предиката A(z) = (z > 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z - 2 < 15) являются все целые числа, меньшие 17.

Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:

Р = А ∩ В = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}.

Его мощность |Р| = 11.

Пример 6. Рассмотрим предикат (50 < х²) → (50 > (х + 1)²), определённый на множестве целых чисел. Найдём множество истинности этого предиката.

Зачастую задания такого рода формулируют несколько иначе.

Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 < х2) → (50 > (х + 1)2)».

Проанализируем отдельно каждый из элементарных предикатов (50 < х²) и (50 > (x + 1)²), решив соответствующие неравенства:

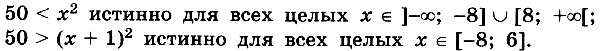
Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):

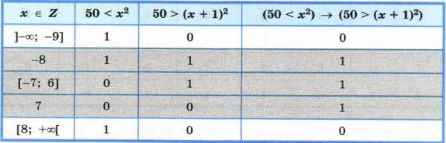
Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.

Cкачать материалы урока