Урок 22
§18. Алгебра логики

САМОЕ ГЛАВНОЕ

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

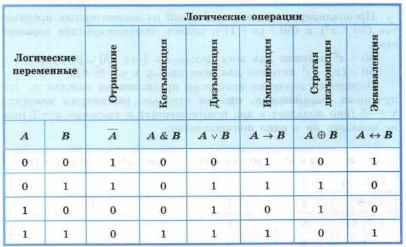
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Логические операции имеют следующий приоритет:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.

Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания

1. Из данных предложений выберите те, которые являются высказываниями. Обоснуйте свой выбор.

1) Как пройти в библиотеку?
2) Коля спросил: «Который час?»
3) Картины Пикассо слишком абстрактны.
4) Компьютеры могут быть построены только на основе двоичной системы счисления.

2. Из каждых трёх выберите два высказывания, являющихся отрицаниями друг друга:

1) «1999 < 2000», «1999 > 2000», «1999 ≤ 2000»;
2) «Петя решил все задания контрольной работы», «Петя не решил все задания контрольной работы», «Петя решил не все задания контрольной работы»;
3) «Луна — спутник Земли», «Неверно, что Луна — спутник Земли», «Неверно, что Луна не является спутником Земли »;
4) «Прямая а не параллельна прямой с», «Прямая а перпендикулярна прямой с», «Прямые а и с не пересекаются» (считаем, что прямые а и с лежат в одной плоскости);
5) «Мишень поражена первым выстрелом», «Мишень поражена не первым выстрелом», «Неверно, что мишень поражена не первым выстрелом».

3. Рассмотрите следующие элементарные высказывания: А = «Река Днепр впадает в Чёрное море», В = «45 — простое число», С = «Вена — столица Австрии», D = «0 — натуральное число».

Определите, какие из них истинные, а какие ложные. Составьте сложные высказывания, применяя каждый раз только одну из пяти логических операций 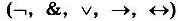к высказываниям А, В, С и D. Сколько новых высказываний можно получить с помощью отрицания (инверсии)? Конъюнкции? Дизъюнкции? Импликации? Эквиваленции? Сколько всего новых высказываний можно получить? Сколько среди них будет истинных?

4. Представьте каждую пословицу в виде сложного логического высказывания, построенного на основе простых высказываний. Ответ обоснуйте при помощи таблиц истинности.

1) На вкус и цвет товарищей нет.
2) Если долго мучиться, что-нибудь получится.
3) Не зная броду, не суйся в воду.
4) Тяжело в ученье, легко в бою.
5) То не беда, что во ржи лебеда, то беда, что ни ржи, ни лебеды.
6) Где тонко, там и рвётся.
7) Или грудь в крестах, или голова в кустах.
8) За двумя зайцами погонишься — ни одного не поймаешь.
9) И волки сыты, и овцы целы.

5. Подберите вместо А, В, С, D такие высказывания, чтобы полученные сложные высказывания имели смысл:

1) если (А или В и С), то D;
2) если (не А и не В), то (С или D);
3) (А или В) тогда и только тогда, когда (С и не D).

6. Вычислите:

1) 1 v X & O;
2) X & X & 1;
3) 0 & X v 0;
4) 0 v X & X.

7. Сколько из приведённых чисел Z удовлетворяют логическому условию: ((Z кратно 4) v (Z кратно 5)) → (Z кратно 6)?
1) 4; 2) 6; 3) 7; 4) 12.

8. Найдите все целые числа Z, для которых истинно высказывание:

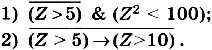
9. Какие из высказываний А, В, С должны быть истинны и ка кие ложны, чтобы были ложны следующие высказывания?

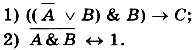
10. Даны три числа в различных системах счисления:

А = 23₁₀, В = 23₈, С = 1А₁₆.

Переведите А, В и С в двоичную систему счисления и вы полните поразрядно логические операции (A v В) & С. Отвеп дайте в десятичной системе счисления.

11. Логическое отрицание восьмиразрядного двоичного числа записанное в десятичной системе счисления, равно 217 Определите исходное число в десятичной системе счисления,

12. Определите логическое произведение и логическую сумм} всех двоичных чисел в диапазоне от 16₁₀ до 22₁₀, включая границы. Ответ запишите в восьмеричной системе счисления.

13. Сколько различных решений имеет логическое уравнение?

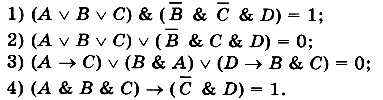
14. Сколько решений имеет логическое уравнение х₁ & х₂ v х₃ & x₄ = 1?

15. Изобразите в декартовой прямоугольной системе координат множества истинности для следующих предикатов:

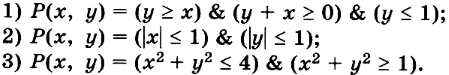
16. Предикат ((8x - 6) < 75) → (х(x - 1) > 65) определён на множестве целых чисел. Найдите его множество истинности. Укажите наибольшее целое число х, при котором предикат превращается в ложное высказывание.

Cкачать материалы урока