Урок 23
§19. Таблицы истинности

19.1. Построение таблиц истинности (продолжение)

Пример 1. Построим таблицу истинности для логического выражения

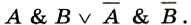
В этом выражении две логические переменные и пять логических операций. Всего в таблице истинности будет пять строк (22 плюс строка заголовков) и 7 столбцов.

Начнём заполнять таблицу истинности с учётом следующего порядка выполнения логических операций: сначала выполняются операции отрицания (в порядке следования), затем операции конъюнкции (в порядке следования), последней выполняется дизъюнкция.

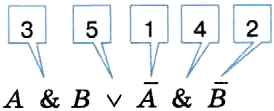
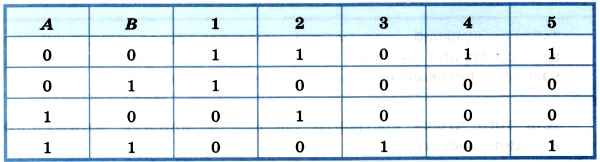
Обратите внимание на последний столбец, содержащий конечный результат. Какой из рассмотренных логических операций он соответствует?

Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают.

Таблица истинности, построенная в предыдущем примере, доказывает равносильность выражений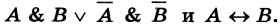

Можно записать: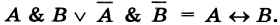

С помощью таблиц истинности докажите равносильность выражений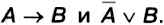

Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.

Cкачать материалы урока