Урок 23
§19. Таблицы истинности

19.2. Анализ таблиц истинности

Рассмотрим несколько примеров.

Пример 2. Известен фрагмент таблицы истинности для логического выражения F, содержащего логические переменные А, В и С.

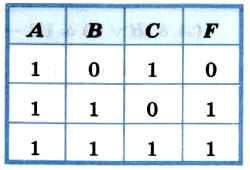
Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?

1) (A v С) & B;
2) (A v B) & (С → А);
3) (А & B v С) & (B → А & С);
4) (А → B) v (С v А → B).

Ответить на поставленный вопрос можно, вычислив значение каждого логического выражения на каждом заданном наборе переменных и сравнив его с имеющимся значением F.

1) Логическое выражение (A v С) & В соответствует данному фрагменту таблицы истинности:

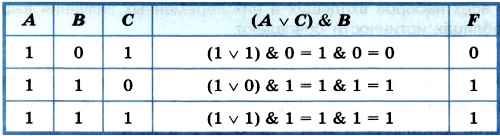
2) Логическое выражение (A v В) & (С → А) не соответствует данному фрагменту таблицы истинности, т. к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.

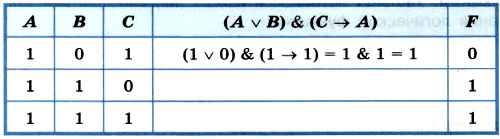
3) Логическое выражение (А & В v С) & (В → А & С) не соответствует данному фрагменту таблицы истинности:

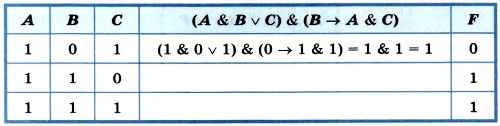
4) Логическое выражение (А → В) v (С v А → В) соответствует данному фрагменту таблицы истинности:

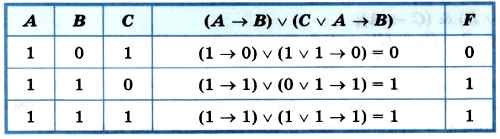
Итак, имеется два логических выражения, соответствующих заданному фрагменту таблицы истинности.

Можно ли утверждать, что в результате решения задачи мы нашли логическое выражение F?

Cкачать материалы урока