Урок 24
§20.1. Основные законы алгебры логики

20.1. Основные законы алгебры логики. Пример 1

Приведём основные законы алгебры логики.

1. Переместительные (коммутативные) законы:

А & В = В & А;

A v В = В v А.

2. Сочетательные (ассоциативные) законы:

(А&В)&С = А&(В&С);

(A v В) v С = A v (В v С).

3. Распределительные (дистрибутивные) законы:

А & (В v С) = (А & В) v (А & С);

A v (В & С) = (A v В) & (A v С).

4. Законы идемпотентности (отсутствия степеней и коэффициентов):

А & А = А;

A v А = А.

5. Закон противоречия:

А & 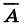= 0.

6. Закон исключённого третьего:

A v 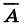= 1.

7. Закон двойного отрицания:

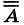= А.

8. Законы работы с константами:

A v 1 = 1; A v O = A;

А & 1 = А; А & 0 = 0.

9. Законы де Моргана:

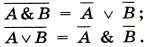
10. Законы поглощения:

А & (A v В) = А;

A v (А & В) = А.

Справедливость законов можно доказать построением таблиц истинности.

Пример 1. Упростим логическое выражение

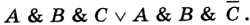
Последовательно применим дистрибутивный закон и закон исключённого третьего:

Cкачать материалы урока