Урок 24
§20.1. Основные законы алгебры логики

20.1. Основные законы алгебры логики. Примеры 2 и 3

Пример 2. Упростим логическое выражение

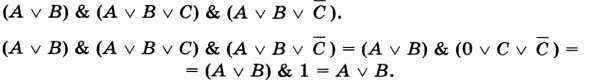
Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:

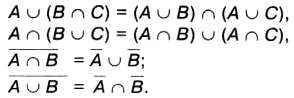
Пробуйте самостоятельно доказать один из этих законов с помощью кругов Эйлера.

Пример 3. На числовой прямой даны отрезки В = [2; 12] и С = [7; 18]. Каким должен быть отрезок А, чтобы предикат 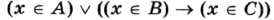становился истинным высказыванием при любых значениях х.

Преобразуем исходное выражение, избавившись от импликации:

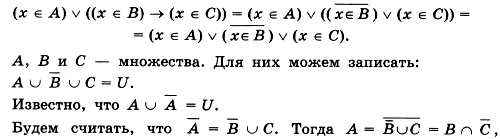^{причём это минимально возможное множество А.}

Множество В — это отрезок [2; 12].

Множество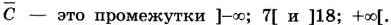

Изобразим это графически:

Пересечением этих множеств будет служить промежуток [2; 7[. В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.

Чему равна минимальная длина отрезка А? Укажите ещё несколько вариантов множества А.

Cкачать материалы урока