Урок 24
§20.1. Основные законы алгебры логики

20.1. Основные законы алгебры логики. Пример 4

Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

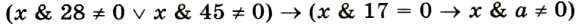
тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.

Прежде всего, вспомним, что представляет собой поразрядная конъюнкция двух целых десятичных чисел, например 27 и 22.

Обратите внимание на то, что если в некотором бите хотя бы одного сомножителя есть 0, то 0 есть и в этом бите результата, а 1 в результате получается только тогда, когда в соответствующих битах каждого сомножителя есть 1.

Введём обозначения:

Перепишем исходное выражение в наших обозначениях:

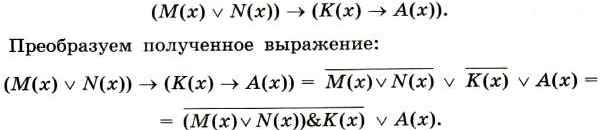
Рассмотрим предикат М(х) = (х & 28 ≠ 0). В числе 28 = 11100₂ 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание х & 28 ≠ 0 будет ложным.

Рассмотрим предикат N(x) = (х & 45 ≠ 0). В числе 45 = 101101₂ 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули.

Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание х & 45 ≠ 0 будет ложным.

Рассмотрим предикат К(х) = (х & 17 = 0). В числе 17 = 10001₂ 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна нулю, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.

По условию задачи надо, чтобы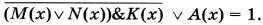

Запишем это выражение для рассмотренных множеств истинности:

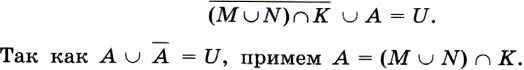
Объединением множеств М и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством К будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т. е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.

Искомое число а должно быть таким, чтобы при любом неотрицательном целом значении переменной х: х & а ≠ 0, и кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 101100₂. Действительно, единицы в нём стоят в тех и только в тех битах, которые нужны для выполнения условия х & а ≠ 0.

Итак, требуемое число 101100₂ или 44₁₀.

Приведите пример такого десятичного числа а, что для него х & а ≠ 0 при любом неотрицательном целом значении десятичной переменной х, но само число а не является минимально возможным.

Пример 5. Выясним, сколько решений имеет следующая система из двух уравнений:

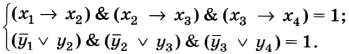
Рассмотрим первое уравнение: (х₁ → х₂) & (х₂ → х₃) & (х₃ → _x4) = 1.

Конъюнкция истинна тогда и только тогда, когда истинны все образующие её высказывания. Следовательно, каждая из трёх входящих в конъюнкцию импликаций должна быть равна 1.

Начнем строить дерево решений, представив на нём значения переменных х₁ и х₂ при которых х₁ → х₂ = 1.

Продолжим строить дерево решений. Значения переменной х₃ будем выбирать такими, чтобы при имеющихся х₂ импликация х₂ → х₃ оставалась истинной.

То же самое проделаем для переменной х₄.

На дереве видно, что рассматриваемое нами уравнение имеет 5 решений — 5 разных наборов значений логических переменных x₁, х₂, х₃, х₄, при которых выполняется равенство:

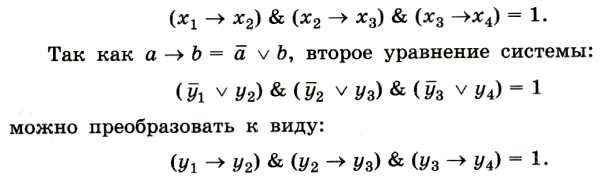
Следовательно, как и первое уравнение, это уравнение имеет 5 решений. Представим их в табличной форме:

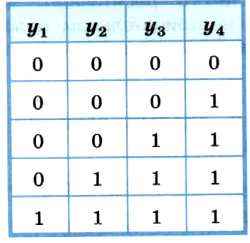
Решение исходной системы логических уравнений — это множество различных наборов значений логических переменных х₁, х₂, х₃, х₄, у₁, у₂, у₃, у₄ таких, что при подстановке каждого из них в систему оба уравнения превращаются в истинные равенства.

Начнём строить такие наборы или двоичные цепочки. Их началом может служить любой из пяти наборов — решений первого уравнения, а концом — любой из пяти наборов — решений второго уравнения. Например, на основе одного из решений первого уравнения можно построить следующие пять решений системы:

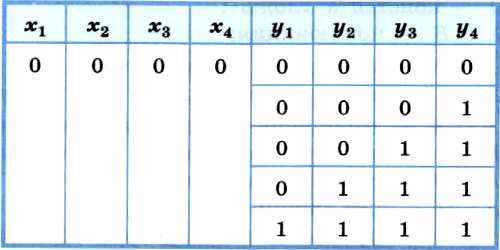
Всего мы можем построить 5 • 5 = 25 решений системы.

Вспомните, как называется теорема комбинаторики, которую мы применили для подсчёта количества решений системы.

Cкачать материалы урока