Уроки 42 - 48
§2.8. Перевод чисел из одной системы счисления в другую

Содержание урока

2.8.1. Перевод целых чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

2.8.2. Перевод дробей из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

2.8.3. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную и обратно

Перевод чисел из двоичной системы счисления в восьмеричную

Перевод чисел из двоичной системы счисления в шестнадцатеричную

Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную

Контрольные вопросы. Задания

2.8.3. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную и обратно

Перевод чисел из двоичной системы счисления в шестнадцатеричную

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. в каждом разряде числа возможны шестнадцать вариантов записи. Решаем показательное уравнение:

16 = 2^I, так как 16 = 2⁴, то I = 4 бита.

Каждый разряд шестнадцатеричного числа содержит 4 бита. Таким образом, для перевода двоичного числа в шестнадцатеричное двоичное число нужно разбить, на группы по четыре цифры. Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных тетрад (групп по 4 цифры) в шестнадцатеричные цифры (табл. 2.3).

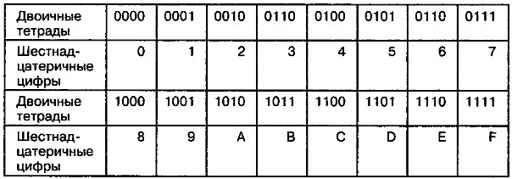
Таблица 2.3. Двоичные тетрады

Перевод целых чисел. Для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа; если в последней левой группе окажется меньше разрядов, надо дополнить ее слева нулями.

Переведем целое двоичное число А2 = 101001₂ в шестнадцатеричное: 0010 1001₂ = 29₁₆.

Перевод дробей. Для перевода дробного двоичного числа в шестнадцатеричное необходимо разбить его на тетрады слева направо; если в последней правой группе окажется меньше чем четыре разряда, необходимо ее дополнить справа нулями.

Переведем дробное двоичное число А₂ = 0,110101₂ в шестнадцатеричную систему счисления: 0,1101 0100₂ = 0,D4₁₆.

Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.

Следующая страница Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную

Cкачать материалы урока