Уроки 63 - 73
§3.2. Алгебра логики
Содержание урока
3.2.1. Логическое умножение, сложение и отрицание
3.2.2. Логические выражения
Практическое задание «Определение истинности логического выражения»
Задание «Таблица истинности логического выражения»
Равносильные логические выражения
Контрольные вопросы. Задания. Компьютерный практикум
3.2.3. Логические функции
3.2.4. Логические законы и правила преобразования логических выражений
3.2.5. Решение логических задач
3.2.2. Логические выражения
Практическое задание «Определение истинности логического выражения»
Определить истинность логического выражения (A ∨ B) & (А ∨ B) с использованием таблиц истинности базовых логических операций и с использованием программного калькулятора.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логического выражения:
(A ∨ B) & (А ∨ B) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
Определение истинности логического выражения т с использованием компьютерного калькулятора
1. Запустить компьютерный калькулятор NumLock Calculator.
2. Установить удобный вид калькулятора командой [Вид калъкулятора-Программистский].
3. Ввести логическое выражение, подставив в него значения логических переменных.
4. Нажать на клавиатуре клавишу {Enter}, получим значение логического выражения (рис. 3.7), которое совпадает со значением, вычисленным с использованием таблиц истинности.
Рис. 3.7. Определение истинности логического выражения с использованием калькулятора
Построение таблиц истинности логических выражений
Для каждого логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений логических переменных.
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то:
Количество строк = 2n.
В нашем случае логическое выражение (A ∨ B) & (А ∨ B) имеет две переменные и, следовательно, количество строк в таблице истинности должно быть равно:
Количество строк = 2n = 22 = 4.
Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций (при желании можно сократить количество столбцов, объединив несколько логических операций в одном столбце). В нашем случае количество переменных равно двум, а количество логических операций равно пяти, т. е. количество столбцов таблицы истинности равно:
Количество столбцов = 2 + 5 = 7.
В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести все возможные наборы значений логических переменных. Наборы входных переменных, во избежание ошибок, рекомендуют вводить следующим образом:
1) разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю — единицами;
2) разделить столбец значений второй переменной на четыре части и заполнить четверти чередующимися группами нулей и единиц, начиная с группы нулей;
3) продолжать деление слолбцов значений последующих переменных на 8, 16 и т. д. частей и заполнение их группами нулей или единиц до тех пор, пока группа нулей (единиц) не будет состоять из одного символа.
В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Построим таблицу истинности для рассмотренного логического выражения (табл. 3.4).
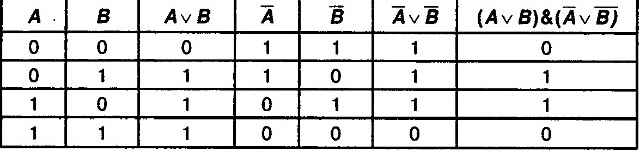
Таблица 3.4. Таблица истинности логического выражения (A ∨ B) & (А ∨ B)
Следующая страница 
Задание «Таблица истинности логического выражения»
Cкачать материалы урока
